首页 Computer-Science Coding-Interviews

# 面试题 27：二叉树的镜像

# 题目

请完成一个函数，输入一棵二叉树，该函数输出它的镜像。二叉树节点的定义如下：

struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
}

# 思路

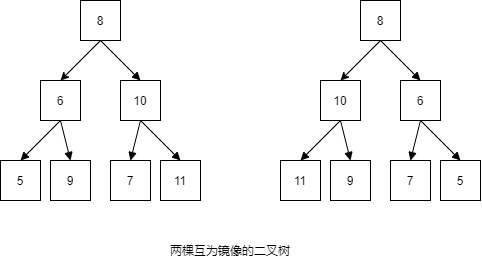
二叉树镜像

通过图像可以看到，互为镜像的两个二叉树的根节点相同，但它们的左、右两个子节点位置相反。对于接下来的节点，依然继续上述的交换过程。

通过总结，我们得出求一棵树的镜像的过程：先前序遍历这棵树的每个节点，如果遍历到的节点有子节点，就交换它的两个子节点。当交换完所有非叶节点的左、右子节点之后，就得到了树的镜像。

# 代码

#include <iostream>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
void mirror_recursively(BinaryTreeNode *node) {
    if (node == nullptr) {
        return;
    }
    if (node->m_left == nullptr && node->m_right == nullptr) {
        return;
    }
    swap(node->m_left, node->m_right);
    if (node->m_left) {
        mirror_recursively(node->m_left);
    }
    if (node->m_right) {
        mirror_recursively(node->m_right);
    }
}
# 面试题 28：对称的二叉树


# 题目


请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。


# 思路


通常我们有 33 种不同的二叉树遍历算法，即前序遍历、中序遍历和后序遍历。在这 33 种遍历算法中，都是先遍历左子节点再遍历右子节点。我们可以定义一种遍历算法，先遍历右子节点再遍历左子节点，可以称之为对称前序遍历。这样，互为镜像的两个二叉树在前序遍历和对称前序遍历下的结果相同。


可以通过比较二叉树的前序遍历序列和对称前序遍历序列来判断二叉树是不是对称的。如果两个序列是一样的，那么二叉树就是对称的。


# 代码


#include <iostream>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
bool is_symmetrical(BinaryTreeNode *root_A, BinaryTreeNode *root_B) {
    if (root_A == nullptr && root_B == nullptr) {
        return true;
    }
    if (root_A == nullptr || root_B == nullptr) {
        return false;
    }
    if (root_A->m_value != root_B->m_value) {
        return false;
    }
    return is_symmetrical(root_A->m_left, root_B->m_right) &&
           is_symmetrical(root_A->m_right, root_B->m_left);
}
bool is_symmetrical(BinaryTreeNode *root) {
    return is_symmetrical(root, root);
}
# 面试题 29：顺时针打印矩阵


# 题目


输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。


例如，如果输入如下矩阵：


(12345678910111213141516)\begin{pmatrix}
 1 & 2 & 3 & 4 \\
 5 & 6 & 7 & 8 \\
 9 & 10 & 11 & 12 \\
 13 & 14 & 15 & 16   
\end{pmatrix}



则依次打印出数字 {1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10}\{1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10\}。


# 思路


参考此  LeetCode  的解析。


# 代码


#include <iostream>
#include <vector>
using namespace std;
vector<int> spiral_order(vector<vector<int>>& matrix) {
    vector <int> ans;
    if(matrix.empty()) return ans; // 若数组为空，直接返回答案
    int u = 0; // 赋值上下左右边界
    int d = matrix.size() - 1;
    int l = 0;
    int r = matrix[0].size() - 1;
    while(true)
    {
        for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); // 向右移动直到最右
        if(++ u > d) break; // 重新设定上边界，若上边界大于下边界，则遍历遍历完成，下同
        for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); // 向下
        if(-- r < l) break; // 重新设定有边界
        for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); // 向左
        if(-- d < u) break; // 重新设定下边界
        for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); // 向上
        if(++ l > r) break; // 重新设定左边界
    }
    return ans;
}
作者：youlookdeliciousc
链接：https://leetcode-cn.com/problems/spiral-matrix/solution/cxiang-xi-ti-jie-by-youlookdeliciousc-3/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
# 面试题 30：包含  min  函数的栈


# 题目


定义桟的数据结构，请在该类型中实现一个能够得到桟的最小元素的  min  函数。在该找中，调用 min 、 push  及  pop  的时间复杂度都是 O(1)O(1)。


# 思路


使用一个辅助栈，当每次有新插入的元素的时候，把每次的最小元素（之前的最小元素和新压入栈的元素两者的较小值）都保存辅助栈里。当弹出元素的时候，将辅助栈中的元素也同时弹出。


# 代码


#include <iostream>
#include <stack>
#include <cassert>
using namespace std;
template<typename T>
class stack_with_min {
public:
    void push(const T &value);
    void pop();
    const T& min() const;
private:
    stack<T> m_data;
    stack<T> m_min;
};
template<typename T>
void stack_with_min<T>::push(const T& value) {
    m_data.push(value);
    if (m_min.empty() || value < m_min.top()) {
        m_min.push(value);
    } else {
        m_min.push(m_min.top());
    }
}
template<typename T>
void stack_with_min<T>::pop() {
    assert(m_data.size() > 0 && m_min.size() > 0);
    m_data.pop();
    m_min.pop();
}
template<typename T>
const T& stack_with_min<T>::min() const {
    assert(m_data.size() > 0 && m_min.size() > 0);
    return m_min.top();
}
# 面试题 31：栈的压入、弹出序列


# 题目


输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5}\{1,2,3,4,5\} 是某栈的压栈序列，序列 {4,5,3,2,1}\{4,5,3,2,1\} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2}\{4,3,5,1,2\} 就不可能是该压栈序列的弹出序列。


# 思路


如果下一个弹出的数字刚好是栈顶数字，那么直接弹出；如果下一个弹出的数字不在栈顶，则把压栈序列中还没有入桟的数字压入辅助栈，直到把下一个需要弹出的数字压入栈顶为止；如果所有数字都压入栈后仍然没有找到下一个弹出的数字，那么该序列不可能是一个弹出序列。


# 代码


#include <iostream>
#include <stack>
#include <vector>
using namespace std;
bool is_pop_order(vector<int> &push_seq, vector<int> &pop_seq) {
    bool is_possible = false;
    if (!push_seq.empty() && !pop_seq.empty()) {
        vector<int>::iterator push_it = push_seq.begin();
        vector<int>::iterator pop_it = pop_seq.begin();
        stack<int> data;
        while (push_it != push_seq.end() && pop_it != pop_seq.end()) {
            while (data.empty() || data.top() != *pop_it) {
                if (push_it != push_seq.end()) {
                    break;
                }
                data.push(*push_it);
                ++push_it;
            }
            if (data.top() != *pop_it) {
                break;
            }
            data.pop();
            ++pop_it;
        }
        if (data.empty() && pop_it == pop_seq.end()) {
            is_possible = true;
        }
    }
    return is_possible;
}
# 面试题 32：从上到下打印二叉树


# 题目一：不分行从上到下打印二叉树


从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。


# 思路


使用队列，打印一个节点时，将其子节点按从左到右的顺序加入队列。直到队列中的元素数量为 00。


# 代码


#include <iostream>
#include <deque>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
void print_from_top_to_bottom(BinaryTreeNode *root) {
    if (root == nullptr) {
        return;
    }
    deque<BinaryTreeNode *> nodes;
    nodes.push_back(root);
    while (!nodes.empty()) {
        BinaryTreeNode *node = nodes.front();
        nodes.pop_front();
        cout << node->m_value << " ";
        if (node->m_left) {
            nodes.push_back(node->m_left);
        }
        if (node->m_right) {
            nodes.push_back(node->m_right);
        }
    }
}
# 题目二：分行从上到下打印二叉树


从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。


# 思路


为了把二叉树的每一行单独打印到一行里，需要有一个变量记录当前层的节点数量。


# 代码


#include <iostream>
#include <queue>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
void print_layer(BinaryTreeNode *root) {
    if (root == nullptr) {
        return;
    }
    queue<BinaryTreeNode *> nodes;
    nodes.push(root);
    while (!nodes.empty()) {
        int size = nodes.size();
        for (int i = 0; i < size; ++i) {
            BinaryTreeNode *node = nodes.front();
            cout << node->m_value << " ";
            nodes.pop();
            if (node->m_left) {
                nodes.push(node->m_left);
            }
            if (node->m_right) {
                nodes.push(node->m_right);
            }
        }
        cout << endl;
    }
}
# 题目三：之字形打印二叉树


请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。


# 思路


按之字形顺序打印二叉树需要两个栈。我们在打印某一层的节点时，把下一层的子节点保存到相应的栈里。如果当前打印的是奇数层（第一层、第三层等），则先保存左子节点再保存右子节点到第一个栈里；如果当前打印的是偶数层（第二层、第四层等），则先保存右子节点再保存左子节点到第二个桟里。


# 代码


#include <iostream>
#include <stack>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
void print_BST_zigzag(BinaryTreeNode *root) {
    if (root == nullptr) {
        return;
    }
    stack<BinaryTreeNode *> levels[2];
    int current = 0;
    int next = 1;
    levels[current].push(root);
    while (!levels[0].empty() || !levels[1].empty()) {
        BinaryTreeNode *node = levels[current].top();
        levels[current].pop();
        cout << node->m_value << " ";
        if (current == 0) {
            if (node->m_left != nullptr) {
                levels[next].push(node->m_left);
            }
            if (node->m_right != nullptr) {
                levels[next].push(node->m_right);
            }
        } else {
            if (node->m_right != nullptr) {
                levels[next].push(node->m_right);
            }
            if (node->m_left != nullptr) {
                levels[next].push(node->m_left);
            }
        }
        if (levels[current].empty()) {
            cout << endl;
            current = 1 - current;
            next = 1 - next;
        }
    }
}
# 面试题 33：二叉搜索树的后序遍历序列


# 题目


输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回  true ，否则返回  false 。假设输入的数组的任意两个数字都互不相同。例如，输入数组 {5,7,6,9,11,10,8}\{5,7,6,9,11,10,8\}，则返回  true 。如果输入的数组是 {7,4,6,5}\{7,4,6,5\}，则由于没有哪棵二叉搜索树的后序遍历结果是这个序列，因此返回  false 。


# 思路


在后序遍历得到的序列中，最后一个数字是树的根节点的值。数组中前面的数字可以分为两部分：第一部分是左子树节点的值，它们都比根节点的值小；第二部分是右子树节点的值，它们都比根节点的值大。


以数组 {5,7,6,9,11,10,8}\{5,7,6,9,11,10,8\} 为例，后序遍历结果的最后一个数字 88 就是根节点的值。在这个数组中，前 33 个数字 55、77 和 66 都比 88 小，是值为 88 的节点的左子树节点；后 33 个数字 99、1111 和 1010 都比 88 大，是值为 88 的节点的右子树节点。


接下来用同样的方法确定与数组每一部分对应的子树的结构。这其实就是一个递归的过程。


# 代码


#include <iostream>
#include <vector>
using namespace std;
bool verify_sequence_of_BST(vector<int> &sequence, int begin, int end) {
    if (sequence.empty()) {
        return false;
    }
    int root = sequence[end - 1];
    // 在二叉搜索树中左子树节点的值小于根节点的值
    int i = begin;
    for ( ; i < end - 1; ++i) {
        if (sequence[i] > root) {
            break;
        }
    }
    // 在二叉搜索树中右子树节点的值大于根节点的值
    int j = i;
    for ( ; j < begin - 1; ++j) {
        if (sequence[j] < root) {
            return false;
        }
    }
    // 判断左子树是否是二叉搜索树
    bool left = true;
    if (i > 0) {
        left = verify_sequence_of_BST(sequence, begin, i);
    }
    // 判断右子树是否是二叉搜索树
    bool right = true;
    if (i < end - 1) {
        right = verify_sequence_of_BST(sequence, begin + i, end);
    }
    return (left && right);
}
# 面试题 34：二叉树中和为某一值的路径


# 题目


输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。


# 思路


当用前序遍历的方式访问到某一节点时，我们把该节点添加到路径上，并累加该节点的值。如果该节点为叶节点，并且路径中节点值的和刚好等于输入的整数，则当前路径符合要求。如果当前节点不是叶节点，则继续访问它的子节点。当前节点访问结束后，递归函数将自动回到它的父节点。因此，我们在函数退出之前要在路径上删除当前节点并减去当前节点的值，以确保返回父节点时路径刚好是从根节点到父节点。


# 代码


#include <iostream>
#include <vector>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
void find_path(BinaryTreeNode *root, int target, vector<int> &path, int current_sum) {
    current_sum += root->m_value;
    path.push_back(root->m_value);
    bool is_leaf = root->m_left == nullptr && root->m_right == nullptr;
    if (current_sum == target && is_leaf) {
        cout << "A path is found: ";
        vector<int>::iterator it = path.begin();
        for ( ; it != path.end(); ++it) {
            cout << *it << "\t";
        }
        cout << endl;
    }
    if (root->m_left != nullptr) {
        find_path(root->m_left, target, path, current_sum);
    }
    if (root->m_right != nullptr) {
        find_path(root->m_right, target, path, current_sum);
    }
    path.pop_back();
}
void find_path(BinaryTreeNode *root, int target) {
    if (root == nullptr) {
        return;
    }
    vector<int> path;
    int current_sum = 0;
    find_path(root, target, path, current_sum);
}