CUDA SGEMM 优化笔记 - CUDA - Computer-Science | Linn's Shoka = 林・初夏 = Linn 的书架

# 前言

本篇博客记录了最近学习的 CUDA 单精度 GEMM 算法的优化过程。

GEMM 算法是指 General Matrix Multiplication 算法，可以说是大多数线性代数算法的基础，也是目前热门的深度学习中最常用的基础计算，因此优化 GEMM 算法对于许多的应用有着重大意义。本篇博客关注的是 NVIDIA 的 GPU 设备上的 GEMM 算法实现，以 cuBLAS 库的算法性能作为比较基线，不断优化算法以逼近该基线。

cuBLAS kernel

# 基础知识

本节将简要介绍 GPU 的计算模型和内存模型的基础知识。因为算法优化部分的内容较长，本节尽量精简。如果之后有时间，后续可能会详细介绍该部分的内容。

# GPU 计算模型

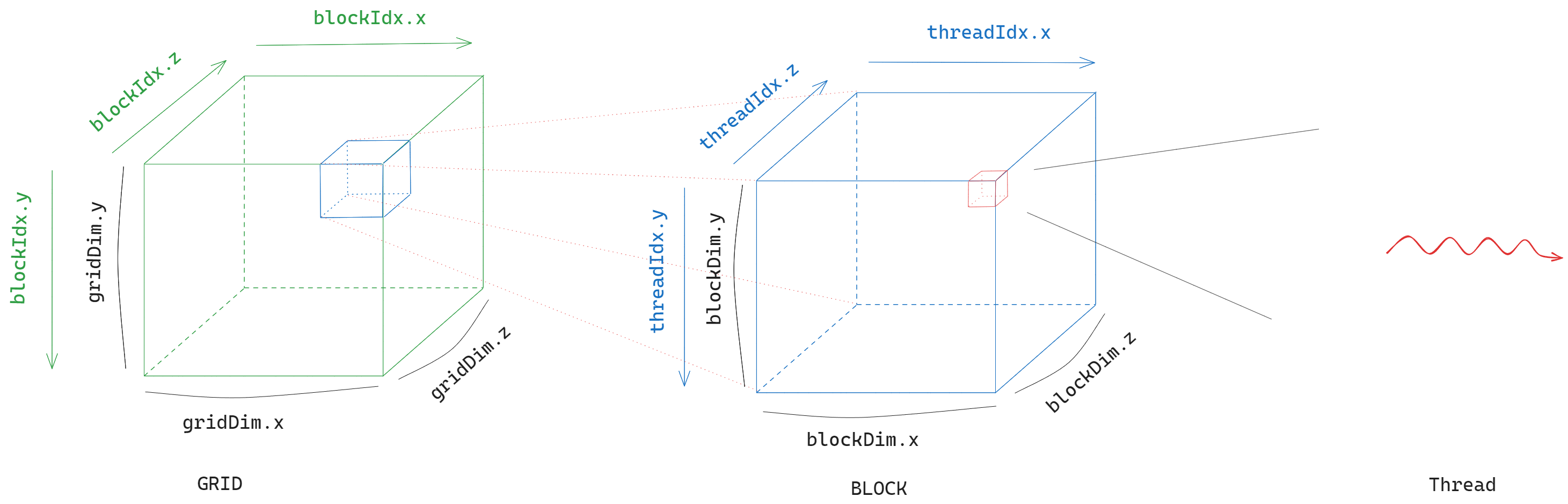
CUDA Computation Model

GPU 的计算模型可以分为上图所示的三级。最基础的执行单元是 thread，用于执行控制单元下发的指令。每个 thread 都属于某一个 block，block 可以有三个维度，在线程中可以通过 CUDA 内置的变量来获取线程对应的 id。每个 block 则又属于一个 grid，grid 也可以有三个维度，有 CUDA 内置变量用于确定 block 的 id。

对于 thread，可以使用 threadIdx.x ， threadIdx.y ， threadIdx.z 获取其在三个维度上的坐标以确定其 “身份”。当然，如果某一个维度的大小为 1，那么我们计算时可以省略。我们可以通过 blockDim.x ， blockDim.y ， blockDim.z 获取线程所在 block 三个维度的大小。类似地，block 可以使用 blockIdx.x ， bloxkIdx.y ， blockIdx.z 获取其在三个维度上的坐标， gridDim.x ， gridDim.y ， gridDim.z 可以获取 block 所在 grid 的三个维度的大小。

而具体到调度层面，需要注意，CUDA 以 block 为单位，将其中的线程调度到某一个 SM（Streaming Multiprocessor）上执行，而在真正执行的时候，CUDA 会将 block 中的线程以 32 个为一个 warp 进行调度，它们的线程 id 连续。如果线程数量不是 32 的倍数，那么 CUDA 会将其补齐。所以我们为每个 block 分配线程时，尽量将数量设置为 32 的倍数。

另外提一句，在访存的时候，会以 half-warp 为单位访存，也就是线程 id 连续的 16 个线程一组进行访存，在考虑 bank conflict 的时候需要注意这一点。

在调用编写的核函数时，我们需要指定 grid 和 block 的维度，一个简单的示例如下：

	// Kernel definition
	__global__ void MatAdd(float A[N][N], float B[N][N], float C[N][N])
	{
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	int j = blockIdx.y * blockDim.y + threadIdx.y;
	if (i < N && j < N)
	C[i][j] = A[i][j] + B[i][j];
	}
	int main()
	{
	...
	// Kernel invocation
	dim3 threadsPerBlock(16, 16);
	dim3 numBlocks(N / threadsPerBlock.x, N / threadsPerBlock.y);
	MatAdd<<<numBlocks, threadsPerBlock>>>(A, B, C);
	...
	}

# GPU 内存模型

GPU 的内存可以分为 off-chip 和 on-chip 内存两大类别。off-chip 的特点是容量大，但是访存延迟高；on-chip 的特点则是容量小，但是访存延迟低。

off-chip 内存主要有 global memory，on-chip 内存则主要有 shared memory 和 register。三者中，register 的访存速度最快，shared memory 次之，global memory 最慢。

CUDA Memory Hierarchy

如上图所示，每个 block 之间共享 global memory，而每个 block 自己则有一块 shared memory，block 中的每个 thread 共享这块 shared memory。此外，每个线程有自己独占的 register 和 local memory，local memory 一般也存放在 global memory 中。

由于 global memory 访存延迟较高，我们很多时候都会将数据读取到 shared memory 中；在某些情况下，甚至会手动使用 register 来缓存 shared memory 中的数据。

可以说，想要优化好 CUDA 上的算法，必须要注意降低或者隐藏访存延迟的开销，在后续的算法优化中我们可以看到这一点。

在调用编写的核函数之前，我们需要使用 cudaMalloc 和 cudaMemcpy 函数来在 GPU 上分配内存，并将 host 侧的数据拷贝到 device 侧。

# GEMM 算法优化

cuBLAS 中实现的通用的 GEMM 算法形式为 $C=\alpha AB+\beta C$ 。其中 $A,B,C$ 均为矩阵，shape 为 $M\times K,K\times N,M \times N$ ， $\alpha$ 和 $\beta$ 为标量。

最简单的实现是 CPU 的串行算法。如果我们对于某个算法在 GPU 中的实现感到难以下手，那么我们可以先从 CPU 算法开始。

	#define OFFSET(row, col, stride) ((row) * (stride) + (col))
	void cpu_naive_matmul(int M, int N, int K, float alpha, float A, float B, float beta, float *C) {
	for (int m = 0; m < M; ++m) {
	for (int n = 0; n < N; ++n) {
	float val = 0.;
	for (int k = 0; k < K; ++k) {
	val += A[OFFSET(m, k, K)] * B[OFFSET(k, n, N)];
	}
	C[OFFSET(m, n, N)] = alpha * val + beta * C[OFFSET(m, n, N)];
	}
	}
	}

# Naive 实现

本节介绍最简单的 CUDA SGEMM 实现，每个线程负责矩阵 $C$ 中的一个元素的计算。

CUDA naive kernel 实现

假定我们启动核函数时的 block 大小为 $BM\times BN$ ，那么我们可以计算每个线程对应的 $C$ 中元素的下标：

	int col = blockIdx.x * blockDim.x + threadIdx.x;
	int row = blockIdx.y * blockDim.y + threadIdx.y;

我们在启动核函数时，一个 grid 中可能会包含多个 block，所以这里还要使用 blockIdx.x ， blockIdx.y 和 blockDim.x 和 blockDim.y 相乘获取每个 block 的基址，即每个 block 最左上方的元素对应的下标。然后再分别加上线程在 block 中的偏移 threadIdx.x 和 threadIdx.y 。

后续的步骤就和 CPU 版本的代码相差无几了：

	if (row < M && col < N) {
	float val = 0.;
	for (int k = 0; k < K; ++k) {
	val += A[OFFSET(row, k, K)] * B[OFFSET(k, col, N)];
	}
	C[OFFSET(row, col, N)] = alpha * val + beta * C[OFFSET(row, col, N)];
	}

这里加上了 if (row < M && col < N) 判断以防越界，因为有时候 $M$ 无法被 $BM$ ，或者 $N$ 无法被 $BN$ 整除。

完整代码如下：

	#define OFFSET(row, col, stride) ((row) * (stride) + (col))
	__global__ void naive_kernel(int M, int N, int K,
	float alpha, float A, float B, float beta, float *C) {
	int col = blockIdx.x * blockDim.x + threadIdx.x;
	int row = blockIdx.y * blockDim.y + threadIdx.y;
	if (row < M && col < N) {
	float val = 0.;
	for (int k = 0; k < K; ++k) {
	val += A[OFFSET(row, k, K)] * B[OFFSET(k, col, N)];
	}
	C[OFFSET(row, col, N)] = alpha * val + beta * C[OFFSET(row, col, N)];
	}
	}

性能比较如下：

naive kernel

可以看到，朴素实现的性能基本都在 1000 GFLOPS 左右，只有 cuBLAS 库性能的十分之一。

我们可以做一个简单的计算。对于矩阵 $C$ 中的每个元素，我们需要访问 $A$ 和 $B$ 中各 $K$ 个元素，总共 $2K$ 次全局内存访问。同时，循环中进行了 $K$ 次乘法和加法共 $2K$ 次运算。计算下来，平均每一次计算就需要一次访存。考虑到 global memory 的访存延迟，这样的做法显然是非常没有效率的。

通过 Nsight Compute 工具也可以看到， warp 花费了大量时间等待全局内存的读写：

naive kernel warp state

切换到代码页面也能看到具体是哪些代码导致了这些 stall。可以发现，我们的核心计算语句耗费了大量时间等待访存读写，这也是我们可以优化的着手点。

naive kernel hotspot code

# 使用 Shared Memory 优化访存

朴素实现中对输入的访问全部都是直接对全局内存进行操作。前文中我们提到，全局内存的访存速度是最慢的，这限制了核函数的计算效率，每个线程耗费了大量的时间等待访存。我们可以尝试使用共享内存来缓存一部分的输入。

可以发现，对于 $C$ 中的每一行元素，在计算过程中都需要访问 $A$ 矩阵中的同一行元素；对于 $C$ 中每一列元素，在计算过程中需要访问 $B$ 矩阵中的同一列元素。那么，对于一个 block 中需要计算的 $BM \times BN$ 元素，有许多对相同地址的重复访问。因此，我们可以使用共享内存预先读取全局内存中所需要的元素，然后计算时直接读取共享内存，节省访存时的等待时间。

CUDA 使用 shared memory 的实现

我们开辟两块 shared memory 中的空间，分别用于存储从 $A$ 和 $B$ 中读取的元素：

	__shared__ float As[BM][BK];
	__shared__ float Bs[BK][BN];

计算时，我们每次需要读取每行或者每列中的 $BK$ 个元素，那么需要迭代 $K/BK$ 次，每次读取 $A$ 和 $B$ 中的一块区域的元素。然后对读取的元素，每个线程使用其所需的元素进行计算。

	float val = 0.;
	int num_shared_block = CEIL_DIV(K, BK);
	A = &A[OFFSET(blockIdx.y * BM, 0, K)]; // Relative position
	B = &B[OFFSET(0, blockIdx.x * BN, N)]; // Relative position
	C = &C[OFFSET(blockIdx.y * BM, blockIdx.x * BN, N)]; // Relative position

	for (int i = 0; i < num_shared_block; ++i) {
	// Copy data from global memory to shared memory
	int A_row = threadIdx.y;
	int A_col = threadIdx.x;
	if ((blockIdx.y * BM + A_row) < M && (i * BK + A_col) < K) {
	As[threadIdx.y][threadIdx.x] = A[OFFSET(A_row, A_col, K)];
	} else {
	As[threadIdx.y][threadIdx.x] = 0.;
	}
	int B_row = threadIdx.y;
	int B_col = threadIdx.x;
	if ((i * BK + B_row) < K && (blockIdx.x * BN + B_col) < N) {
	Bs[threadIdx.y][threadIdx.x] = B[OFFSET(B_row, B_col, N)];
	} else {
	Bs[threadIdx.y][threadIdx.x] = 0.;
	}
	__syncthreads();
	A += BK; // Add offset
	B += BK * N; // Add offset
	for (int k = 0; k < BK; ++k) {
	val += As[threadIdx.y][k] * Bs[k][threadIdx.x];
	}
	__syncthreads();
	}

注意上述代码中，我们为三个矩阵的指针添加了偏移量，后续计算坐标时，只需要计算其在子矩阵中的相对位置即可。不过也要注意，在判断是否越界时，需要转换为全局的下标，否则会判断错误。

每次迭代中，我们只计算了 $C$ 中对应元素值的一部分，待到迭代完毕，便得到了最终的结果。注意迭代过程中，使用了 __syncthreads() 来同步每个线程，防止数据读取不同步，造成读取的数据错误。

最后，将计算结果写回：

	int C_row = threadIdx.y;
	int C_col = threadIdx.x;
	if ((blockIdx.y * BM + C_row) < M && (blockIdx.x * BN + C_col) < N) {
	C[OFFSET(C_row, C_col, N)] = alpha * val + beta * C[OFFSET(C_row, C_col, N)];
	}

shared memory kernel

emmm，理论上而言，每个 block 需要从全局内存中读取 $\frac{K}{BK}\times(BM\times BK + BK\times BN)$ 个浮点数。而朴素算法中，一个 block 总共需要 $2K\times BM \times BN$ 次访存。可以看到，使用了一维 Tile 方法之后，访存降为了原来的 $\frac{1}{2}(\frac{1}{BN}+\frac{1}{BM})$ 。一般有 $BM=BN$ ，因此，全局内存访问将为了原来的 $\frac{1}{BM}$ 。而每个线程的计算量不变，则计算访存比也降低为原来的 $\frac{1}{BN}$ 。不过从我测试的结果来看，和 naive 的结果比较并没有明显的区别，甚至还变差了一丢丢。

shared memory kernel warp state

可以看到，这次是 Stall MIO Throttle 这一项的 stall cycles 最多。这一项根据文档说明，一般是某些特殊的数学计算函数、动态分支、共享内存读写导致的，放在我们的上下文中，那就可以肯定是共享内存导致的瓶颈，在横轴上几乎和使用全局内存的代码一致，数值也很接近。这也是为什么这段代码和直接使用全局代码的性能几乎没有变化。

# 一维 Tile

要进一步优化，可以从前文的 profiling 结果入手。我们无论是使用全局内存还是共享内存，主要的瓶颈都在访存上。为了进一步掩盖访存开销，我们要么可以提高访存的效率，要么让每个线程的负载更多一点，以使得能够掩盖访存的开销。

这里我们先尝试提高每个线程的负载，让每个线程多计算一些元素的输出。这里我们让每个线程计算矩阵 $C$ 一列中连续几个元素的值。

一维 Tile

在使用共享内存的基础上，我们添加了一维 Tile 的代码。

float val[TM] = {0.};

因为每个线程需要计算 $TM$ 个元素的结果，我们使用一个 $TM$ 大小的数组来存储中间结果。

在拷贝数据时，每个线程需要在 $A$ 矩阵中多拷贝 $TM$ 次：

	// Copy data from global memory to shared memory
	for (int m = 0; m < TM; ++m) {
	int A_row = threadIdx.y * TM + m;
	int A_col = threadIdx.x;
	if ((blockIdx.y * BM + A_row) < M && (i * BK + A_col) < K) {
	As[A_row][A_col] = A[OFFSET(A_row, A_col, K)];
	} else {
	As[A_row][A_col] = 0.;
	}
	}

计算中间结果时，也需要多一层循环：

	for (int k = 0; k < BK; ++k) {
	for (int m = 0; m < TM; ++m) {
	int A_row = threadIdx.y * TM + m;
	int B_col = threadIdx.x;
	val[m] += As[A_row][k] * Bs[k][B_col];
	}
	}

最后，将计算结果写回：

	for (int m = 0; m < TM; ++m) {
	int C_row = threadIdx.y * TM + m;
	int C_col = threadIdx.x;
	if ((blockIdx.y * BM + C_row) < M && (blockIdx.x * BN + C_col) < N) {
	C[OFFSET(C_row, C_col, N)] = alpha * val[m] + beta * C[OFFSET(C_row, C_col, N)];
	}
	}

1d tile kernel

可以看到，使用 Tile 之后，性能得到了一定的提升，逼近了 2000 GFLOPS。一个 block 全局访存的数量依然为 $K(M+N)$ ，但是每个线程负责的计算量为原来的 $TM$ 倍，因此计算访存比提升了 $TM$ 倍。

tile 1d kernel warp state

这次可以看到，相比仅使用共享内存，增加线程计算负载之后 Stall MIO Throttle 这一项的横轴数值有了减小，之前超过了 20 cycles per instruction，现在已经在 20 以下了。不过也可以看出，这一项的延时依然较高，我们还可以有提升空间。

# 二维 Tile

和一维 Tile 类似，这次我们让每个线程负责计算矩阵 $C$ 中一小块 $TM \times TN$ 区域中的元素，进一步提升每个线程的负载。有了一维 Tile 的代码，我们简单地在其基础之上做少许修改，便可以得到二维 Tile 的代码。

存储中间结果需要分配 $TM \times TN$ 大小的空间：

float val[TM][TN] = {0.};

注意这里的 $TM$ 和 $TN$ 不能设置过大，否则可能寄存器资源不够，导致 register spill，这时中间数据便会使用 local memory 存储，访存速度会慢很多。

拷贝数据时，在矩阵 $B$ 上也要多拷贝 $TN$ 次：

	for (int n = 0; n < TN; ++n) {
	int B_row = threadIdx.y;
	int B_col = threadIdx.x * TN + n;
	if ((i * BK + B_row) < K && (blockIdx.x * BN + B_col) < N) {
	Bs[B_row][B_col] = B[OFFSET(B_row, B_col, N)];
	} else {
	Bs[B_row][B_col] = 0.;
	}
	}

同理，计算结果时需要使用二重循环：

	for (int k = 0; k < BK; ++k) {
	for (int m = 0; m < TM; ++m) {
	int A_row = threadIdx.y * TM + m;
	for (int n = 0; n < TN; ++n) {
	int B_col = threadIdx.x * TN + n;
	val[m][n] += As[A_row][k] * Bs[k][B_col];
	}
	}
	}

结果写回：

	for (int m = 0; m < TM; ++m) {
	int C_row = threadIdx.y * TM + m;
	for (int n = 0; n < TN; ++n) {
	int C_col = threadIdx.x * TN + n;
	if ((blockIdx.y * BM + C_row) < M && (blockIdx.x * BN + C_col) < N) {
	C[OFFSET(C_row, C_col, N)] = alpha * val[m][n] + beta * C[OFFSET(C_row, C_col, N)];
	}
	}
	}

2d tile kernel

可以看到，现在的性能相比朴素的实现有了很大的提升，性能接近了 4000 GFLOPS。在一维 Tile 的基础之上，计算访存比进一步提升了 $TN$ 倍。

tile 2d kernel warp state

可以看到，现在的 Stall MIO Throttle 已经降低到 11 cycles per instruction。相比仅使用共享内存，降低到了原来的不到一半。性能的数值也和 profiling 的结果能够互相印证。

# 使用寄存器进一步优化访存

对于二维 Tile 中计算矩阵 $C$ 结果的代码：

	for (int k = 0; k < BK; ++k) {
	for (int m = 0; m < TM; ++m) {
	int A_row = threadIdx.y * TM + m;
	for (int n = 0; n < TN; ++n) {
	int B_col = threadIdx.x * TN + n;
	val[m][n] += As[A_row][k] * Bs[k][B_col];
	}
	}
	}

可以看到，对于 As 中的内容重复访问了 $TN$ 次；对于 Bs 中的内容，在外层的 m 迭代中，也会重复访问 $TM$ 次。因此，我们可以使用寄存器将这部分内容缓存下来，进一步提升访存。

	for (int k = 0; k < BK; ++k) {
	for (int m = 0; m < TM; ++m) {
	int A_row = threadIdx.y * TM + m;
	As_cache[m] = As[A_row][k];
	}
	for (int n = 0; n < TN; ++n) {
	int B_col = threadIdx.x * TN + n;
	Bs_cache[n] = Bs[k][B_col];
	}
	for (int m = 0; m < TM; ++m) {
	for (int n = 0; n < TN; ++n) {
	val[m][n] += As_cache[m] * Bs_cache[n];
	}
	}
	}

不过这部分的优化在我的测试中对性能的提升并不明显。

在 profiling 的结果中发现，和使用之前对于 Stall MIO Throttle 指标几乎没有降低，也就是并没有降低访存的开销。

从代码对应图中可以看到，虽然我们使用了寄存器，但是从共享内存读取数据到寄存器中的时候依然存在较大的 MIO 延迟，即这个延迟只是从一条语句转移到了其他语句之上，并没有被我们掩盖掉，所以没有性能提升也就是正常的了。

# 使用 FLOAT4 指令优化访存

tile 2d performance analysis

通过前面 profiling 的结果，能够发现很大一部分时间仍然花在了等待访存之上。可以看到，内存带宽的使用负载大于计算的负载。访存延迟依然是程序性能的瓶颈。

我们可以进一步利用 GPU float4 访存特性来进一步优化，让每个元素一次获取 4 个浮点数，进一步减少访存次数。相比于访存 4 次获取 4 个浮点数，通过 float4 向量内存指令所需的访存指令数更少，减少了对内存访问的竞争；另一方面，使用向量加载每个字节需要的索引计算更少，我们只需要计算一次索引即可读取 4 个浮点数。但是这样一来，代码也会变得略显复杂。

同时，我们在读取矩阵 $A$ 的内容时，还要对其进行转置，然后再存储到 shared memory 中，以方便后续线程计算时使用 float4 读取，以避免共享内存的 bank conflict。

我们使用以下宏来定义一次访问 4 个浮点数的操作：

#define FETCH_FLOAT4(pointer) (reinterpret_cast<float4*>(&(pointer))[0])

需要注意，因为使用了 FLOAT4 访存的缘故，矩阵的元素数量必须是 4 的倍数，不再能够支持任意大小的矩阵^[1]。

对于 As 缓存，其分配的空间能够存储 $BM\times BK$ 个浮点数，在一个 block 中共有 $(BM/TM)\times (BN/TN)$ 个线程，每个线程一次读取 4 个浮点数，那么总共需要读取 $\frac{BM\times BK}{BM/TM\times BN/TN \times 4}$ 次；同理， Bs 缓存需要读取 $\frac{BK\times BN}{BM/TM\times BN/TN \times 4}$ 。

	const int block_row_thread = BN / TN;
	const int block_col_thread = BM / TM;
	const int thread_num = block_row_thread * block_col_thread;
	const int load_a_cache_time = (BK * BM) / thread_num / 4; // Each thread load 4 float
	const int load_b_cache_time = (BK * BN) / thread_num / 4; // Each thread load 4 float

使用 float4 访存

如上图所示，假设 $BK=16$ ，共有 $8$ 个线程，那么一次读取就能够读完 As 中的两行。那么每个线程下一次读取时间隔的行数就是 $8/(BK/4)=2$ 。

其实，我们不妨把 As 看成一个矩阵元素是 float4 的矩阵，那么原来的 As 就相当于一个大小为 $BM\times (BK/4)$ 大小的新矩阵 As_new 。那么，我们可以根据线程的 id 来计算其对应放置的地址偏移，我们不妨把线程看成一维的，这样更方便计算。

首先，计算出线程的 id：

int thread_id = threadIdx.y * blockDim.x + threadIdx.x;

As 中每一行需要 $BK/4$ 个线程读取，那么线程对应的行数为：

int a_tile_row = thread_id / (BK / 4);

同理，对应的列数为 thread_id % (BK / 4) 。不过这是 As_new 中地址便宜，换算回 As 还得乘 4，也就是：

int a_tile_col = thread_id % (BK / 4) * 4;

按照上述方式，我们也可以计算得出 Bs 的对应偏移：

	int b_tile_row = thread_id / (BN / 4);
	int b_tile_col = thread_id % (BN / 4) * 4;

上述计算的地址是每次读取的子矩阵中的相对偏移，每次读取时，我们还需要添加一个基址偏移。对于 As ，共有 $BM$ 行，上面计算得到了共需要读取 load_a_cache_time ，那么可以知道每次需要偏移的大小为：

int a_tile_stride = BM / load_a_cache_time;

同理， Bs 中的对应大小为：

int b_tile_stride = BK / load_b_cache_time;

在读取 As 时，注意还需要对其进行转置，其代码如下：

	for (int i = 0; i < BM; i += a_tile_stride) {
	int cache_idx = i / a_tile_stride * 4;
	FETCH_FLOAT4(load_a_cache[cache_idx]) =
	FETCH_FLOAT4(A[OFFSET(a_tile_row + i, a_tile_col, K)]);
	// Use load_a_cache for load 4 float at a time
	// As is saved as transpose matrix
	As[a_tile_col][a_tile_row + i] = load_a_cache[cache_idx];
	As[a_tile_col + 1][a_tile_row + i] = load_a_cache[cache_idx + 1];
	As[a_tile_col + 2][a_tile_row + i] = load_a_cache[cache_idx + 2];
	As[a_tile_col + 3][a_tile_row + i] = load_a_cache[cache_idx + 3];
	}

这里开辟了一个寄存器缓存 load_a_cache ，作为转置时的临时存放空间，其大小为 load_a_cache_time * 4 。注意下面为每次读取单独开辟了空间存储，而不是复用之前的空间。我在测试的时候发现，如果复用之前的空间，会因为数据写入地址的依赖导致计算结果出错。

float load_a_cache[4 * load_a_cache_time];

每次读取时， $A$ 矩阵的基础行偏移量为循环变量中的 i ，其每次变化 a_tile_stride ，在此基础之上，每个线程本身还需要添加一个行偏移量 a_tile_row ，和列偏移量 a_tile_col 。每次读取 4 个元素，将其存放在 load_a_cache 中的对应位置， cache_idx 可以由 i / a_tile_stride * 4 计算得到， i / a_tile_stride 表示迭代的次数，乘 4 表示每次存放 4 个元素。

读取之后，我们将 load_a_cache 中的元素转置存放在 As 中，注意下标的计算。

类似地， Bs 的读取代码如下：

	for (int i = 0; i < BK; i += b_tile_stride) {
	FETCH_FLOAT4(Bs[b_tile_row + i][b_tile_col]) =
	FETCH_FLOAT4(B[OFFSET(b_tile_row + i, b_tile_col, N)]);
	}

因为 Bs 不需要转置，我们可以直接将其存放在 Bs 对应位置中。

注意上述代码中的 A 和 B 都预先添加了偏移量， C 也是：

	A = &A[OFFSET(blockIdx.x * BN;, 0, K)]; // Set block start position
	B = &B[OFFSET(0, blockIdx.y * BM;, N)];
	C = &C[OFFSET(blockIdx.x * BN, blockIdx.y * BM, N)];

后续的计算基本和二维 Tile 中的代码一致，只不过我们会一次性读取 4 个浮点数：

	for (int i = 0; i < BK; ++i) {
	for (int m = 0; m < TM; m += 4) {
	FETCH_FLOAT4(As_cache[m]) = FETCH_FLOAT4(As[i][ty + m]);
	}
	for (int n = 0; n < TN; n += 4) {
	FETCH_FLOAT4(Bs_cache[n]) = FETCH_FLOAT4(Bs[i][tx + n]);
	}
	for (int m = 0; m < TM; ++m) {
	for (int n = 0; n < TN; ++n) {
	accum[m][n] += As_cache[m] * Bs_cache[n];
	}
	}
	}

注意本文的所有 for 循环代码中，为了简洁，去掉了每个 for 循环上的 #pragma unroll 循环展开指令。实际中可以添加该指令进一步提升指令吞吐。

后续写回结果，也可以使用 float4 来减少访存次数：

	float tmp[4] = {0.};
	for (int m = 0; m < TM; ++m) {
	for (int n = 0; n < TN; n += 4) {
	FETCH_FLOAT4(tmp) = FETCH_FLOAT4(C[OFFSET(ty + m, tx + n, N)]);
	tmp[0] = alpha * accum[m][n] + beta * tmp[0];
	tmp[1] = alpha * accum[m][n + 1] + beta * tmp[1];
	tmp[2] = alpha * accum[m][n + 2] + beta * tmp[2];
	tmp[3] = alpha * accum[m][n + 3] + beta * tmp[3];
	FETCH_FLOAT4(C[OFFSET(ty + m, tx + n, N)]) = FETCH_FLOAT4(tmp);
	}
	}

性能对比如下：

float4 kernel

可以看到，使用 float4 访存之后性能得到了很大的提升。每个线程的计算量并没有改变，但是现在每次可以读取 4 个浮点数，全局内存访问次数进一步降低了四分之一。而且指令的执行效率也提升。相比于访存 4 次获取 4 个浮点数，通过 float4 向量内存指令所需的访存指令数更少，减少了对内存访问的竞争；另一方面，使用矢量加载每个字节需要的索引计算更少。这些是隐形的对性能的提升。

float4 kernel warp state

从 profiling 结果可以看到，通过使用 float4 访存基本上消除了 MIO 的延迟。图中的其他指标的延迟也在 1~1.5 cycles per instruction 之间。

# 数据预取

在上文的代码中，我们在循环中使用了两次 __syncthreads() 来做线程同步，以防止不同线程之间的数据不一致。其中第一个 __syncthreads() 是为了保证写后读（Read-After-Write）的顺序性，这个是无法避免的。

关键在于后一个同步，它是为了防止部分线程还未读取 As 或者 Bs 中的内容，保证读后写（Write-After-Read）的顺序性。它本质上是因为我们在不同迭代中使用了同一块空间来保存我们所需的数据，这两次迭代中的数据之间并不存在真正的依赖关系。如果我们将其写入到其他地址上，那么就不需要使用同步了。

这种方式称为数据预取，又可以称为双缓存（Double Buffering）。我们可以申请两倍所需的空间，用于在迭代中交替使用，从而省去后一次线程同步的操作。

	__shared__ float As[2][BK][BM]; // transpose shared A for avoid bank conflict, for double buffering
	__shared__ float Bs[2][BK][BN]; // for double buffering

	float As_cache[2][TM] = {0.}; // double buffering
	float Bs_cache[2][TN] = {0.}; // double buffering

在迭代中，我们可以使用一个变量来控制写入的地址：

	int write_idx = 0;

	for (int k = 0; k < K; k += BK) {
	for (int i = 0; i < BM; i += a_tile_stride) {
	int cache_idx = i / a_tile_stride * 4;
	FETCH_FLOAT4(load_a_cache[cache_idx]) =
	FETCH_FLOAT4(A[OFFSET(a_tile_row + i, a_tile_col, K)]);
	// Use load_a_cache for load 4 float at a time
	// As is saved as transpose matrix
	As[write_idx][a_tile_col][a_tile_row + i] = load_a_cache[cache_idx];
	As[write_idx][a_tile_col + 1][a_tile_row + i] = load_a_cache[cache_idx + 1];
	As[write_idx][a_tile_col + 2][a_tile_row + i] = load_a_cache[cache_idx + 2];
	As[write_idx][a_tile_col + 3][a_tile_row + i] = load_a_cache[cache_idx + 3];
	}
	...

	for (int i = 0; i < BK; i += b_tile_stride) {
	FETCH_FLOAT4(Bs[write_idx][b_tile_row + i][b_tile_col]) =
	FETCH_FLOAT4(B[OFFSET(b_tile_row + i, b_tile_col, N)]);
	}
	__syncthreads();

	...

	for (int i = 0; i < BK; ++i) {
	for (int m = 0; m < TM; m += 4) {
	FETCH_FLOAT4(As_cache[write_idx][m]) = FETCH_FLOAT4(As[write_idx][i][ty + m]);
	}
	for (int n = 0; n < TN; n += 4) {
	FETCH_FLOAT4(Bs_cache[write_idx][n]) = FETCH_FLOAT4(Bs[write_idx][i][tx + n]);
	}
	for (int m = 0; m < TM; ++m) {
	for (int n = 0; n < TN; ++n) {
	accum[m][n] += As_cache[write_idx][m] * Bs_cache[write_idx][n];
	}
	}
	}

	...

	write_idx ^= 1;
	}

性能对比如下：

double buffer kernel

使用双缓冲之后，因为避免了多一次的线程同步，性能得到了进一步提升。

# 避免 Shared Memory Bank Conflict

经过以上的优化，我们的性能已经非常接近 cuBLAS 的基线了。

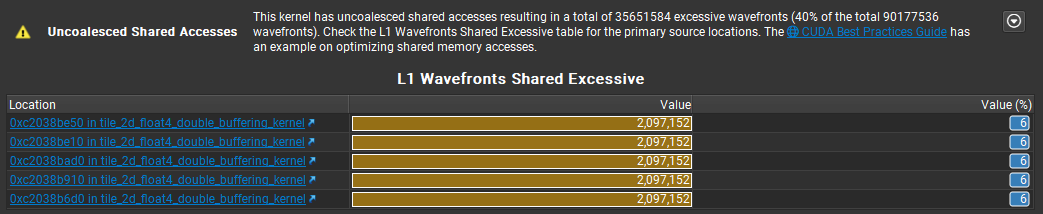
shared memory bank conflict

但是通过 profiling 可以看到，对共享内存的访问上有 40% 的 Uncoalsced Memory Access。这说明共享内存的访问上存在许多 bank conflict。我们可以使用这篇矩阵优化笔记中的思路来解决这一问题。

我们在通过 Tile 计算的过程中，计算的都是矩阵 $C$ 中的连续区域的值，我们可以通过 interleaved 的方式，进一步对其分块^[2]：

避免 shared memory bank conflict

对应到代码中，我们从 As 和 Bs 中读取数据时，不再是连续的一整块数据，而是以 4 为单位间隔读取：

	for (int k = 0; k < BK; ++k) {
	for (int m = 0, mm = 0; m < BM && mm < TM; m += block_row_thread * 4, mm += 4) {
	int A_row = m + threadIdx.y * 4;
	FETCH_FLOAT4(As_cache[write_idx][mm]) = FETCH_FLOAT4(As[write_idx][k][A_row]);
	}
	for (int n = 0, nn = 0; n < BN && nn < TN; n += block_col_thread * 4, nn += 4) {
	int B_col = n + threadIdx.x * 4;
	FETCH_FLOAT4(Bs_cache[write_idx][nn]) = FETCH_FLOAT4(Bs[write_idx][k][B_col]);
	}
	...
	}

而在写回结果时也要注意对矩阵 $C$ 的下标计算：

	for (int m = 0; m < TM; m += 4) {
	int C_row = (m / 4) * (block_row_thread * 4) + threadIdx.y * 4;
	for (int n = 0; n < TN; n += 4) {
	int C_col = (n / 4) * (block_col_thread * 4) + threadIdx.x * 4;
	for (int i = 0; i < 4; ++i) {
	FETCH_FLOAT4(load_a_cache) = FETCH_FLOAT4(C[OFFSET(C_row + i, C_col, N)]);
	load_a_cache[0] = alpha * accum[m + i][n] + beta * load_a_cache[0];
	load_a_cache[1] = alpha * accum[m + i][n + 1] + beta * load_a_cache[1];
	load_a_cache[2] = alpha * accum[m + i][n + 2] + beta * load_a_cache[2];
	load_a_cache[3] = alpha * accum[m + i][n + 3] + beta * load_a_cache[3];
	FETCH_FLOAT4(C[OFFSET(C_row + i, C_col, N)]) = FETCH_FLOAT4(load_a_cache);
	}
	}
	}

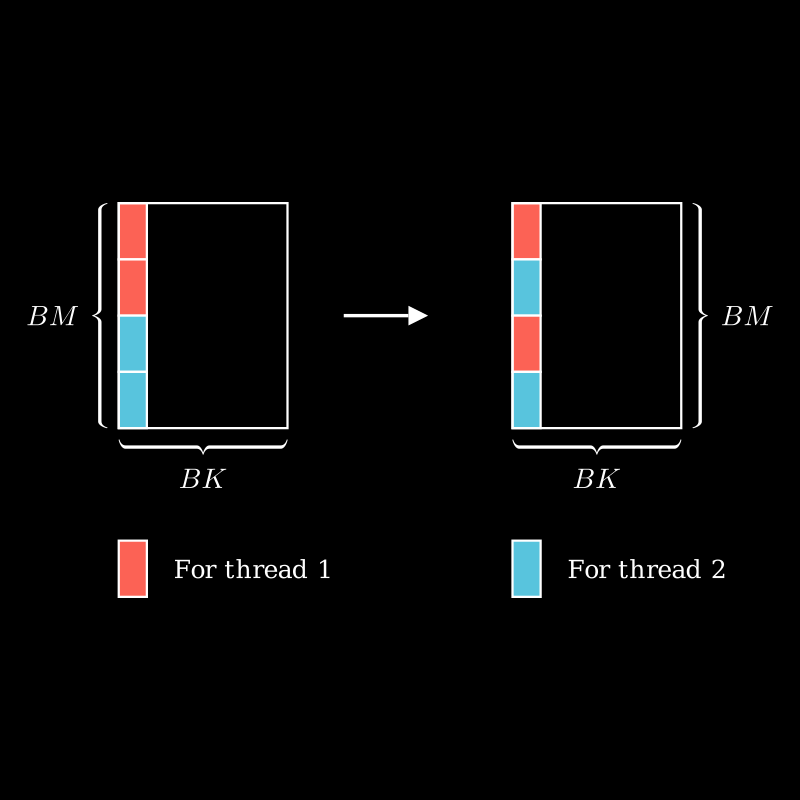
access pattern to avoid shared memory bank conflict

m 和 n 除以 4 是因为读取时以 4 个浮点数为一组读取，这 4 个浮点数对应的行是相邻的，每 4 行之后，就需要跳跃到下一个对应的位置，乘以 (block_row_thread * 4) 和 (block_col_thread * 4) 即是为此。

在行和列上分别有 block_row_thread 和 block_col_thread 个线程，那么当前线程下一次操作的数据的行和列的起始位置就是 (m / 4) * (block_row_thread * 4) 和 (n / 4) * (block_col_thread * 4) 。

最后，再添加当前线程自己在行和列上的偏移 threadIdx.y * 4 和 threadIdx.x * 4 。

对于 n 可以使用 float4 的方式读取和写入，而对于 m ，我们需要再使用一层循环写入相邻的行中。

kernel avoid shared memory bank conflict

可以看到，在大矩阵上，现在的性能基本和 cuBLAS 持平了。我们也基本实现了我们的性能优化目标。

# 寄存器 bank 冲突

在处理共享内存 bank 冲突的基础之上，其实还能够进一步考虑处理寄存器的 bank 冲突^[3]^[4]。不过这部分内容过于复杂，需要使用到 SASS 的 CUDA 汇编代码。这里就不去具体实现了，仅在这里记录一下。

# 性能对比总结

这里以 $4096\times 4096$ 大小矩阵的性能总结各个优化和 cuBLAS 库的性能比较。

Kernel	Ratio to cuBLAS
cublas	1
naive	0.106
shared memory	0.091
tile 1d	0.158
tile 2d	0.352
float4	0.857
double buffering	0.912
avoid shared memory bank conflict	0.995

# 总结

这次国庆假期前前后后断断续续花费了 5 天完成了这篇优化笔记。前两天几乎全部花在代码编写上，后面三天断断续续完成了文章的内容。为了完成这篇内容，这期间参考了许多的笔记和资料^[5]^[6]^[7]，最后总算也得到了一个很好的优化结果。之前一直都是单纯的资料阅读，这次的实践确实收获颇丰，自己动手编写代码和直接调用别人的接口感觉确实有很大不同。CUDA 编程也需要了解更多的硬件相关的知识，这次实践中也了解了不少。“纸上得来终觉浅，绝知此事要躬行”。后续可能进一步考虑学习其他深度学习的重要算子的优化。

本次的代码放在我的仓库上了，可供参考。

以上。

# Change Log

2023-10-14：补充 Nsight Compute profiling 结果，修正部分文本错误和措辞
2023-10-15：重绘一些插图

# 附录

# CLion CUDA 编程配置

使用 CLion 创建 CUDA 工程， CMakeLists.txt 内容如下：

	cmake_minimum_required(VERSION 3.22)
	project(sgemm LANGUAGES CXX CUDA)

	set(CMAKE_CUDA_STANDARD 20)
	set(CMAKE_CUDA_FLAGS "-O3")
	# For debug
	# set(CMAKE_CUDA_FLAGS "-g -G")
	# For Nsight Compute Profiling
	# set (CMAKE_CUDA_FLAGS "${CMAKE_CUDA_FLAGS} -lineinfo")

	find_package(CUDAToolkit REQUIRED)

	add_executable(${PROJECT_NAME} main.cu
	src/utils.cu
	src/kernels.cu)

	# 可执行文件输出路径
	# https://gist.github.com/gavinb/c993f71cf33d2354515c4452a3f8ef30
	set(EXECUTABLE_OUTPUT_PATH ${PROJECT_SOURCE_DIR})

	set_target_properties(${PROJECT_NAME} PROPERTIES
	CUDA_SEPARABLE_COMPILATION ON)
	# 查询 compute capability https://developer.nvidia.com/cuda-gpus
	set_target_properties(${PROJECT_NAME} PROPERTIES CUDA_ARCHITECTURES "86")

	# 配置头文件搜索路径
	# 配置 CUDA 相关库头文件
	# 参考
	# https://stackoverflow.com/questions/51756562/obtaining-the-cuda-include-dir-in-c-targets-with-native-cuda-support-cmake
	target_include_directories(${PROJECT_NAME} PRIVATE ${CMAKE_CUDA_TOOLKIT_INCLUDE_DIRECTORIES})
	target_include_directories(${PROJECT_NAME} PUBLIC ${PROJECT_SOURCE_DIR}/src)

	# link cudart cublas
	target_link_libraries(${PROJECT_NAME} PRIVATE CUDA::cublas)

此外，需要在 Settings -> Build,Execution,Deployment -> CMake 中的 CMake options 中添加以下参数：

-DCMAKE_CUDA_COMPILER=/usr/local/cuda/bin/nvcc

# cuBLAS 库接口调用

使用 cuBLAS 的矩阵乘法接口 cublasSgemm 函数时，需要注意其参数传递^[8]。

具体的封装参考如下：

	void test_cublas(cublasHandle_t handle, int M, int N, int K,
	float alpha, float A, float B, float beta, float *C) {
	//cublas 列主序计算：https://www.cnblogs.com/cuancuancuanhao/p/7763256.html
	cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &alpha, B, N, A, K, &beta, C, N);
	}

# CUDA 程序性能 Profiling

CUDA 性能 profiling 可以去官网^[9]下载 Nsight Compute 和 Nsight System 工具。其中 System 用于粗粒度的性能分析，Compute 用于对核函数的细粒度性能分析。

实际上，对于非 4 的倍数的元素个数，也是可以使用 float4 来访存的，但是在边界条件判断上需要更细致的处理，对性能也会有一定的影响。 ↩︎
图片来自于这篇知乎的矩阵优化笔记 ↩︎
CUDA 知识点：bank 冲突 | CUDA - zhongtian's blog (zh0ngtian.tech) ↩︎
深入浅出 GPU 优化系列：GEMM 优化（三） - 知乎 (zhihu.com) ↩︎
CUDA SGEMM 矩阵乘法优化笔记 —— 从入门到 cublas - 知乎 (zhihu.com) ↩︎
wangzyon/NVIDIA_SGEMM_PRACTICE: Step-by-step optimization of CUDA SGEMM (github.com) ↩︎
How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog (siboehm.com) ↩︎
有关 CUBLAS 中的矩阵乘法函数 - 爨爨爨好 - 博客园 (cnblogs.com) ↩︎
Gameworks Download Center | NVIDIA Developer ↩︎