首页Computer-ScienceCUDACUTLASS

# 前言

CUTLASS（CUDA Templates for Linear Algebra Subroutines and Solvers）是 NVIDIA 的一个用于高性能矩阵计算的 CUDA 库，类似于 cuBLAS 和 cuDNN。它将数据移动等操作封装成了 C++ 模板，帮助开发者在 NVIDIA GPU 上实现高效的线性代数操作。支持 Tensor Core 矩阵运算，FP32/TF32/FP16/BF16/FP64/Int4/Int8/Int1 等多种类型的数据格式。目前大模型中的 Flash Attention 算法就是基于 CUTLASS 实现的。

CUTLASS 的 3.0 版本提出了一套新的用于描述 Tensor 排布的模板库，并封装了许多数据索引相关的运算。这篇文章将会介绍一些 CuTe 相关的基础概念，如果想要更加深入了解，可以参看知乎用户 reed 的系列文章[1][2]。

# CuTe

计算机的内存是一个一维的线性地址空间，我们通常所用的矩阵或者更高维度的 Tensor 的坐标，都需要经过映射对应到其真实的物理内存地址。在目前常见的深度学习框架中，通常都采用 Shape 和 Stride 的形式来描述一个 Tensor 的坐标到物理地址的映射。而 CuTe 的描述形式则是基于这个 Shape 和 Stride 形式拓展而来的 Hierarchy Tensor 。相比于简单的 Shape 和 Stride ，这种描述形式可以表达更为复杂的映射关系。

接下来我们将通过一些例子来展现这两种描述方式的能力差异。

# Shape + Stride

目前深度学习框架中通常使用的都是 Shape + Stride 的形式来描述逻辑地址和实际物理地址的映射关系。以一个二维矩阵为例，常用的内存排布模式有「行优先」和「列优先」两种，下面是一个 Shape 为 (2, 4) 的矩阵在两种情形下的内存排布：

row-major

col-major

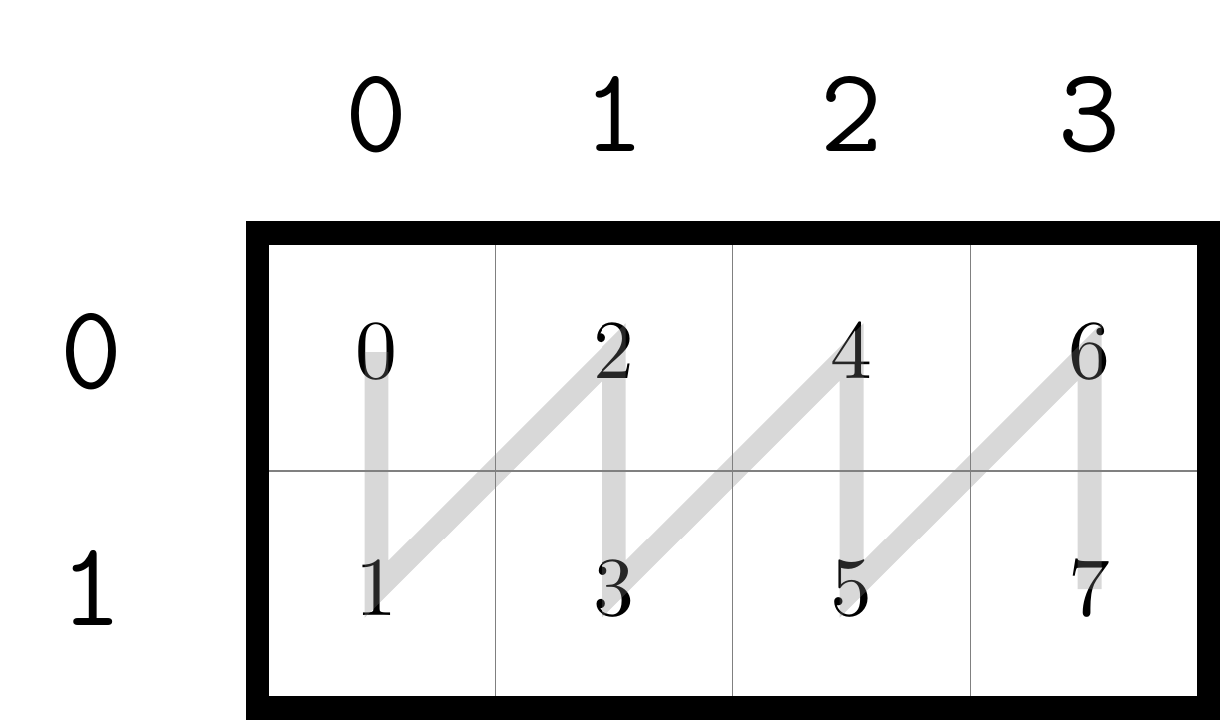
图中每个方格中的数字表示该位置元素在内存中按顺序排列时的下标。可以看到，相同的矩阵下标位置，在不同的排布方式，其在内存中的顺序可能是不同的。例如，矩阵坐标 (1, 0) 在行优先和列优先的情况下，对应元素在内存中的顺序分别是 4 和 1 （从 0 开始计数）。在大部分编程语言中，常用的排布方式是行优先，例如 C/C++ ，列优先方式一般是 Fortran 。在 Python 的 numpy 库中，创建 tensor 时默认是行优先，可以传入 order="F" 参数指定使用列优先排布。

我们在编写循环遍历矩阵时，一般都会将第二个下标作为内层循环，就是因为通常的矩阵都采用行优先排布。如果是列优先排布，那么就需要将第二个下标的循环放在外层以保证数据的局部性。

这里的矩阵的 Shape 就是 (2, 4) ，而 Stride 则用于区分不同的排布：

  • 行优先： Shape (2, 4) + Stride (4, 1)
  • 列优先： Shape (2, 4) + Stride (1, 2)

如果要根据矩阵的坐标对应的内存地址映射，则将坐标 (i, j) 与 Stride 对应的元素相乘再求和即可。例如 (1, 0) 的坐标在行优先和列优先对应的内存地址映射就是分别和 Stride (4, 1) 以及 (1, 2) 相乘再求和的结果，这与我们在图中所见的结果一致。

# Hierarchy Tensor

上述 Shape + Stride 的描述方式在常见情况下基本能够满足使用，但是在 CUDA 编写中可能会遇到更复杂的内存排布情况无法用这种方式来表述。Graphene[3] 这篇论文提出了一种新的层次化的排布表述方式。我们可以看下面的 4 个例子：

Layout A-col-major

Layout B-row-major

Layout C

Layout D

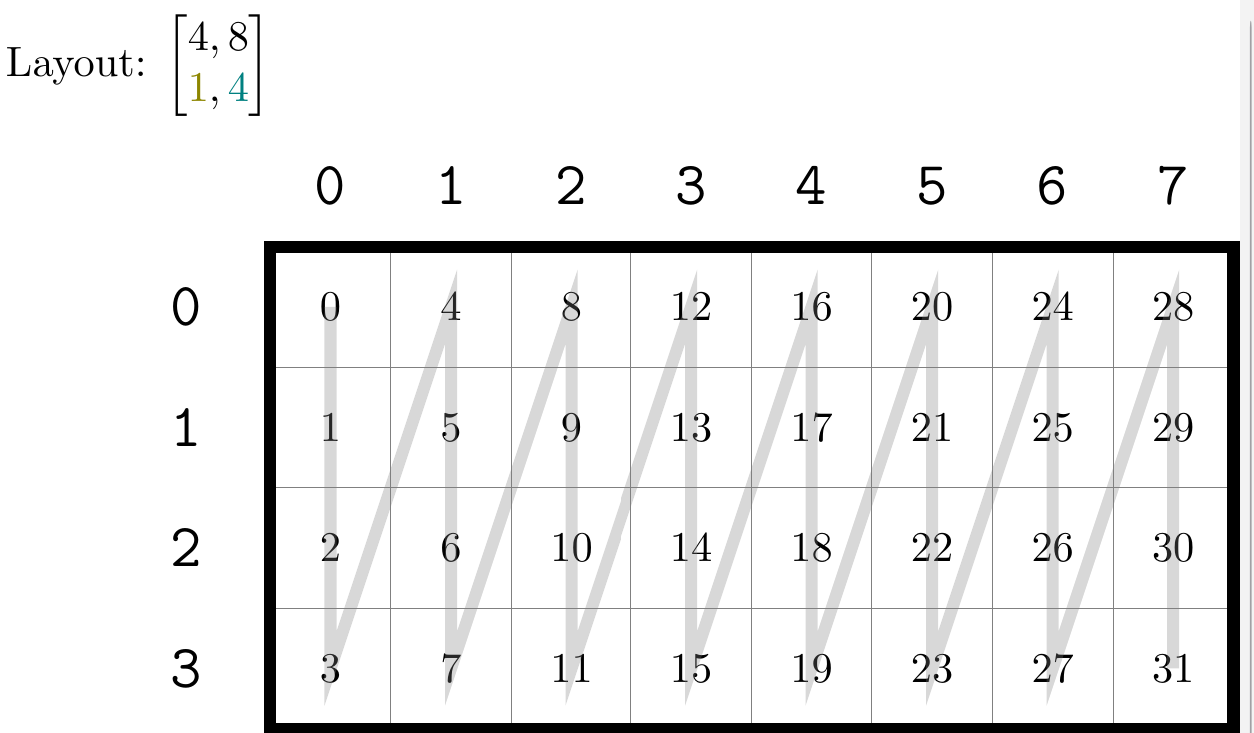
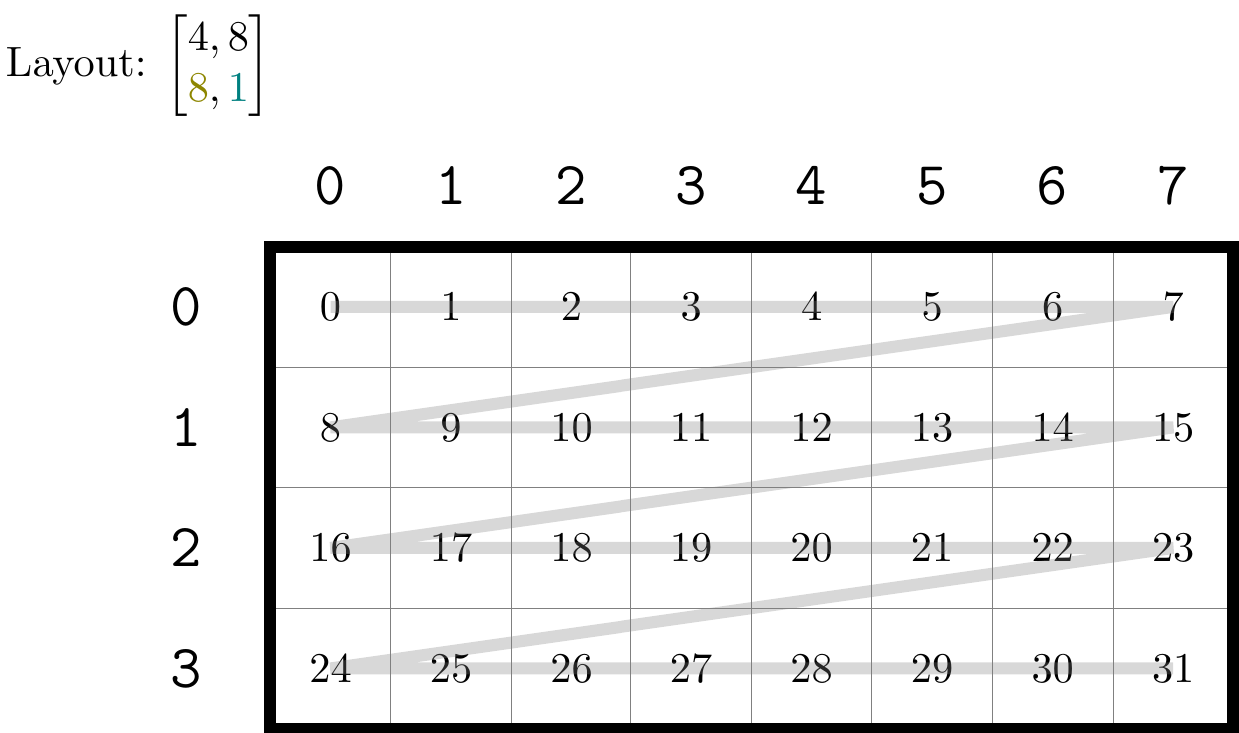
这里先解释一下 Layout 的表述格式。在图片中，使用类似矩阵的形式来表达 Layout ，第一行是 Shape ，第二行是 Stride 。可以看到行优先和列优先的表述，与上文的 Shape + Stride 表述是一致的，也就是其能够兼容这种表述方式。而 C 和 D 两种排布方式则是原有的 Shape + Stride 无法表达的情形。 C 和 D 中的 Shape 和 Stride 是嵌套的，通常的 Shape 或者 Stride 中的元素是一个单独的整数，而层次化表述中，元素可以是一个元组。

那么，这种嵌套的情形应该如何直观理解？对于第一行的 Shape ， C 和 D 中的元素虽然有元组，但是他们的元素个数依然是 2 个，即上述 4 个例子的 Shape 的 rank 均为 2 （ CuTe 中使用 rank 来表述元素的个数），也就是一个整数和一个元组对于计数的贡献是一样的。上述 4 个矩阵都能够用二维的图形来表述，因为他们的 rank 是 2。

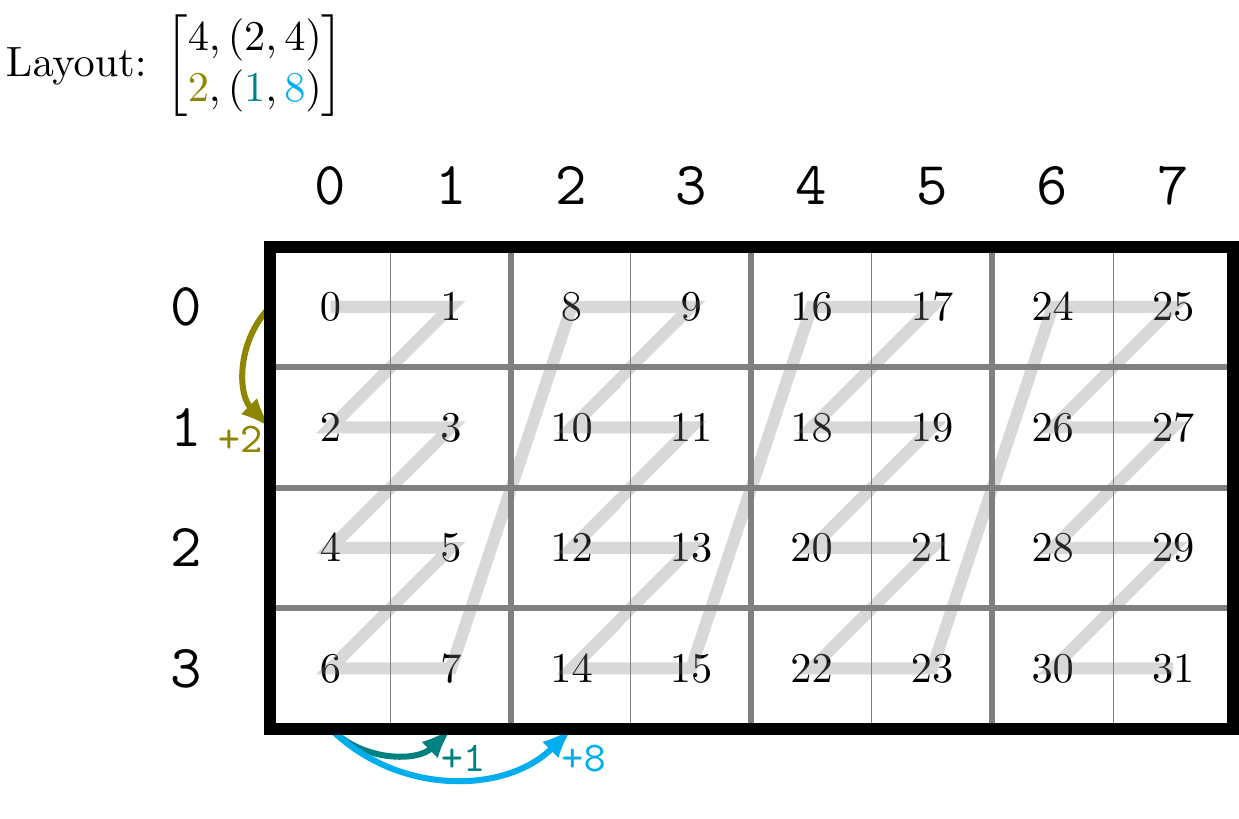
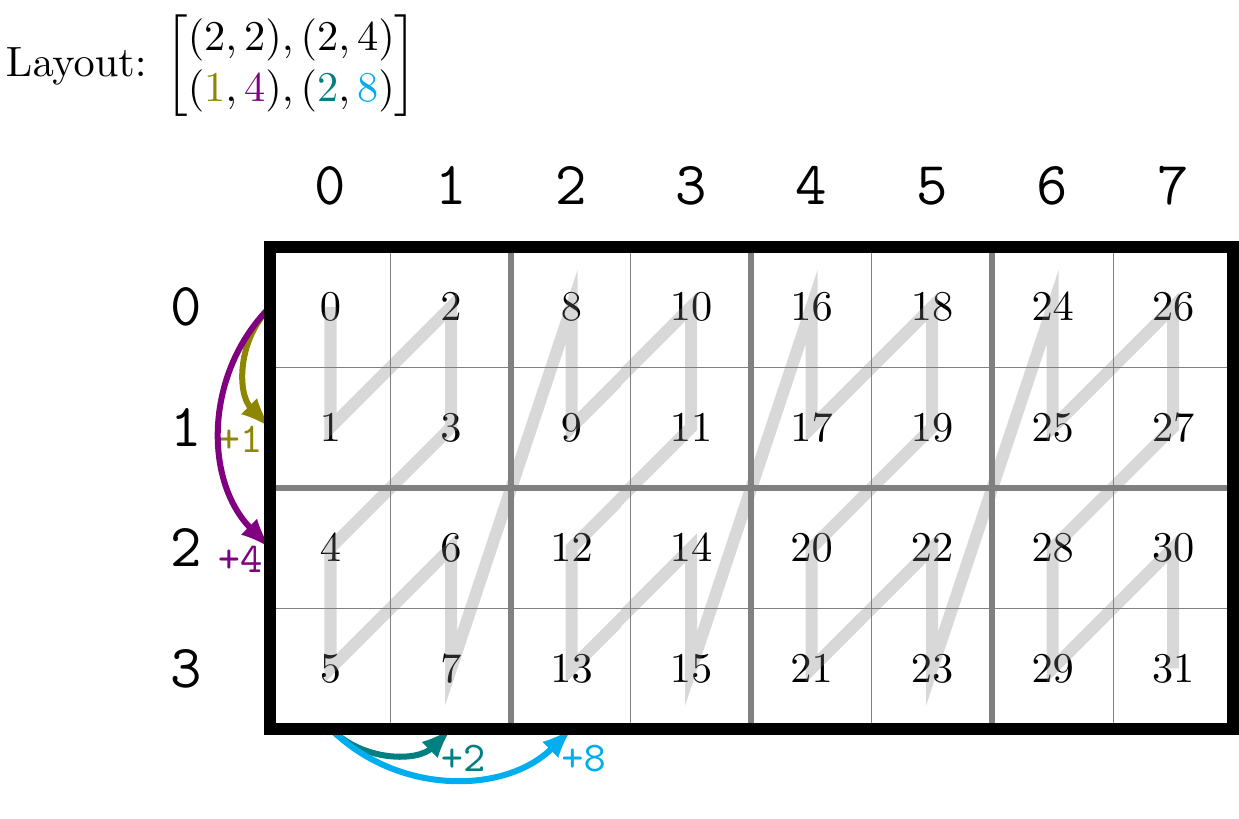
以最中间的逗号分隔，第一个元素描述的是行上的层次分布，第二个元素描述的是列上的层次分布。如果元素是整数，那么就和通常的矩阵描述一致，例如上面的 A B 以及 C 中的第一个元素，均描述了这个矩阵有几行。而如果元素是一个元组，那么其中描述的就是不同层次中矩阵的行数。以 D 为例，其第一个元素为 (2, 2) ，这两个 2 分别描述了内层矩阵和外层矩阵的行数。内层矩阵为内部用灰色粗线包裹的矩阵，如 [0,21,3]\begin{bmatrix} 0, & 2\\1, & 3 \end{bmatrix} 这个矩阵，这个矩阵行数为 2。而外层矩阵则是将内层矩阵视为一个「元素」时的行数。例如 D 中在行方向有 [0,21,3]\begin{bmatrix} 0, & 2\\1, & 3 \end{bmatrix} 和 [4,65,7]\begin{bmatrix} 4, & 6\\5, & 7 \end{bmatrix} 这两个矩阵，故行数也为 2。由此我们可以总结出第一个元素的表述方式是 (r0,r1,⋯ ,rn)(r_0, r_1, \cdots, r_n)，其中每个 rir_i 表示由内而外第 ii 层的矩阵的行数，列的描述也同理。

故对于 (r0,r1,⋯ ,rn),(c0,c1,⋯ ,cn)(r_0, r_1, \cdots, r_n), (c_0, c_1, \cdots, c_n) 表示的 Shape ，第 ii 个行 - 列对 (ri,ci)(r_i, c_i) 表示的是将 (r0,r1,⋯ ,ri−1),(c0,c1,⋯ ,ci−1)(r_0, r_1, \cdots, r_{i-1}), (c_0, c_1, \cdots, c_{i-1}) 为 Shape 的矩阵视为一个元素时，矩阵的行数和列数分别为 rir_i 和 cic_i。

再看 Stride ，其每个元素与 Shape 中的元素对应，表示该对应维度下，相邻元素「首地址」在内存地址上的间隔。例如 C 中，在行方向移动一格，其内存地址相差 2；在内层列上移动一格，内存地址相差 1；在外层列上移动一个，内存地址相差 8。 D 的表述同理。图片中用箭头表示了每个维度相邻元素首地址差。

计算实际的内存地址时，只需要将 Shape 与 Stride 对应元素相乘求和即可，这与 Shape + Stride 表述方式的计算是一致的。

# 总结

这篇文章介绍了 CuTe 这一种新的 Tensor 逻辑地址和物理地址的映射方式。上文种介绍的主要是二维的情形，理论上更高维也可以描述，但是已经不方便直观理解了。从我目前看到的相关内容来看，二维的情况占了绝大多数。本篇文章是基于自己个人理解的表述，可以参看知乎用户 reed 的「cute 之 Layout」[1:1]这篇文章。

本文的图片使用的代码基于 CUTLASS 库官方代码修改而来的 pycute 库[4]，放在我的个人仓库中，有需要可以自取。

  1. cute 之 Layout ↩︎ ↩︎

  2. cute Layout 的代数和几何解释 ↩︎

  3. Graphene: An IR for Optimized Tensor Computations on GPUs ↩︎

  4. pycute ↩︎