首页 Computer-Science Coding-Interviews

# 面试题 7：重建二叉树

# 题目

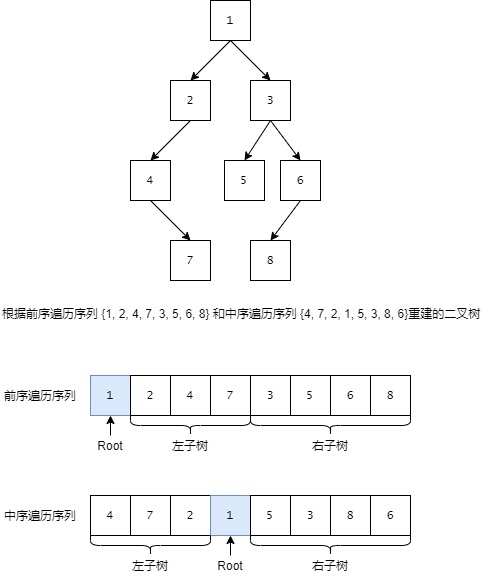
输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如，输入前序遍历序列 {1,2,4,7,3,5,6,8}\{1,2,4,7,3,5,6,8\} 和中序遍历序列{4,7,2,1,5,3,8,6}\{4,7,2,1,5,3,8,6\}，则重建如图所示的二叉树并输出它的头节点。二叉树节点的定义如下：

struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
}

binary_tree_rebuild

# 思路

在二叉树的前序遍历序列中，第一个数字总是树的根节点的值。但在中序遍历序列中，根节点的值在序列的中间，左子树的节点的值位于根节点的值的左边，而右子树的节点的值位于根节点的值的右边。因此我们需要扫描中序遍历序列，才能找到根节点的值。

根据前序遍历序列，我们能够找到当前树的根节点；然后在中序遍历序列中，根据根节点的位置，判断左子树和右子树的节点数量。由此可以在前序遍历的序列中确定左子树和右子树的分界点。之后，对于左子树和右子树重复上述过程，即可完成重建。

# 代码

#include <iostream>
#include <vector>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
BinaryTreeNode *build_core(vector<int>::iterator pre_begin, vector<int>::iterator pre_end,
                           vector<int>::iterator in_begin, vector<int>::iterator in_end) {
     if (pre_begin == pre_end || in_begin == in_end) {
        return nullptr;
    }
    int root_val = *pre_begin;
    BinaryTreeNode *root = new BinaryTreeNode();
    root->m_value = root_val;
    root->m_left = root->m_right = nullptr;
    vector<int>::iterator root_inorder_it = in_begin;
    while (root_inorder_it < in_end && *root_inorder_it != root_val) {
        ++root_inorder_it;
    }
    if (root_inorder_it == in_end) {
        return nullptr;
    }
    int left_len = root_inorder_it - in_begin;
    int right_len = in_end - root_inorder_it - 1;
    if (left_len > 0) {
        root->m_left = build_core(pre_begin + 1, pre_begin + left_len + 1, in_begin, root_inorder_it);
    }
    if (right_len > 0) {
        root->m_right = build_core(pre_begin + left_len + 1, pre_end, root_inorder_it + 1, in_end);
    }
    return root;
}
BinaryTreeNode *build(vector<int> preorder, vector<int> inorder) {
    if (preorder.empty() || inorder.empty() || preorder.size() != inorder.size()) {
        return nullptr;
    }
    return build_core(preorder.begin(), preorder.end(), inorder.begin(), inorder.end());
}#include <iostream>
#include <vector>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
};
BinaryTreeNode *build_core(vector<int>::iterator pre_begin, int pre_len,
                           vector<int>::iterator in_begin, int in_len) {
    int root_val = *pre_begin;
    BinaryTreeNode *root = new BinaryTreeNode();
    root->m_value = root_val;
    root->m_left = root->m_right = nullptr;
    if (pre_len == 1) {
        if (in_len == 1 && *pre_begin == *in_begin) {
            return root;
        } else {
            throw exception("Invalid input.");
        }
    } else if (pre_len != in_len) {
        throw exception("Invalid input.");
    }
    vector<int>::iterator root_inorder_it = in_begin;
    while (root_inorder_it < in_begin + in_len && *root_inorder_it != root_val) {
        ++root_inorder_it;
    }
    if (root_inorder_it == in_begin + in_len) {
        throw exception("Invalid input.");
    }
    int left_len = root_inorder_it - in_begin;
    int right_len = in_len - left_len - 1;
    if (left_len > 0) {
        root->m_left = build_core(pre_begin + 1, left_len, in_begin, left_len);
    }
    if (right_len > 0) {
        root->m_right = build_core(pre_begin + left_len + 1, right_len, in_begin, right_len);
    }
    return root;
}
BinaryTreeNode *build(vector<int> preorder, vector<int> inorder) {
    if (preorder.empty() || inorder.empty() || preorder.size() != inorder.size()) {
        return nullptr;
    }
    return build_core(preorder.begin(), preorder.size(), inorder.begin(), inorder.size());
}
# 面试题 8：二叉树的下一个节点


# 题目


给定一棵二叉树和其中的一个节点，如何找出中序遍历序列的下一个节点？树中的节点除了有两个分别指向左、右子节点的指针，还有一个指向父节点的指针。


# 思路


如果一个节点有右子树，那么它的下一个节点就是它的右子树中的最左节点。


如果一个节点没有右子树，并且是其父节点的左子节点，那么它的下一个节点就是它的父节点。


如果一个节点没有右子树，并且是其父节点的右子节点，那么需要沿着父节点遍历，直到找到一个节点，这个节点是它的父节点的左子节点。如果这样的节点不存在，说明最开始的节点是树中的最右节点，没有下一个节点。


上述的下一个节点，即一个节点的后继 (successor)；对应地，前一个节点称为前驱 (predecessor)。


针对不同的遍历方式，如前序遍历和后序遍历，前驱和后继表示的节点也不相同，这里暂时不详细讨论。


# 代码


#include <iostream>
#include <vector>
using namespace std;
struct BinaryTreeNode {
    int m_value;
    BinaryTreeNode *m_left;
    BinaryTreeNode *m_right;
    BinaryTreeNode *m_parent;
};
BinaryTreeNode *inorder_successor(BinaryTreeNode *node) {
    if (node == nullptr) {
        return nullptr;
    }
    BinaryTreeNode *next = nullptr;
    // 如果节点有右子树，寻找右子树的最左节点
    if (node->m_right != nullptr) {
        BinaryTreeNode *right = node->m_right;
        while (right->m_left != nullptr) {
            right = right->m_left;
        }
        next = right;
    } else if (node->m_parent != nullptr) {
        BinaryTreeNode *cur = node;
        BinaryTreeNode *parent = node->m_parent;
        while (parent != nullptr && cur == parent->m_right) {
            cur = parent;
            parent = parent->m_parent;
        }
        next = parent;
    }
    return next;
}
# 面试题 9：用两个栈实现队列


# 题目


用两个栈实现一个队列。队列的声明如下，请实现它的两个函数  append_tail  和  delete_head ，分别完成在队列尾部插入节点和在队列头部删除节点的功能。


template<typename T> class Queue {
public:
    Queue();
    ~Queue();
    void append_tail(const T& node);
    T delete_head();
private:
    stack<T> stack1;
    stack<T> stack2;
}
# 思路


对于两个栈  stack1  和  stack2 ， stack1  用于插入元素，而  stack2  则用于删除元素。


当有元素插入时，直接插入到  stack1  中；


当删除元素时，如果  stack2  为空，则将  stack1  中的元素依次弹出插入到  stack2  中，这时  stack2  中的元素出栈的顺序和  stack1  中的元素入栈的顺序一致，即模拟了队列的先进先出的性质；而如果  stack2  不为空，此时栈顶的元素对应队列的队首元素，可以直接删除栈顶的元素。


# 代码


#include <iostream>
#include <stack>
using namespace std;
template<typename T> class Queue {
public:
    Queue();
    ~Queue();
    void append_tail(const T& element);
    T delete_head();
private:
    stack<T> stack1;
    stack<T> stack2;
};
template<typename T>
void Queue<T>::append_tail(const T &element) {
    stack1.push(element);
}
template<typename T>
T Queue<T>::delete_head() {
    if (stack2.size() <= 0) {
        while (stack1.size() > 0) {
            T &data = stack1.top();
            stack1.pop();
            stack2.push(data);
        }
    }
    if (stack2.size() == 0) {
        throw "Queue is empty";
    }
    T head = stack2.top();
    stack2.pop();
    return head;
}