首页 Computer-Science Coding-Interviews

# 面试题 10：斐波那契数列

# 题目一：求斐波那契数列的第 nn 项

写一个函数，输入 nn，求斐波那契 (Fibonacci) 数列的第 nn 项。斐波那契数列的定义如下：

f(n)={0,n=0;1,n=1;f(n−1)+f(n−2),n>1f(n) = \begin{cases} 0, & n = 0; \\ 1, & n = 1; \\ f(n-1) + f(n-2), & n > 1 \end{cases}

# 思路

递归解法很容易解决这个问题，但是递归的时间复杂度是指数级别的。

从公式可以看出，斐波那契数列的每一项只和前两项有关，因此在计算的时候，可以利用数组记录前两项，从过这两项计算出下一项的数字。之后更新数组。

另一个 O(log⁡n)O(\log n) 的思路是通过矩阵乘法来实现。这个方法基于以下的公式：

[f(n)f(n−1)f(n−1)f(n−2)]=[1110]n−1\begin{bmatrix} f(n) & f(n-1) \\ f(n-1) & f(n-2) \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^{n-1}

通过以上公式，只需要求得 [1110]n−1\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^{n-1} 即可得到 f(n)f(n)。而求矩阵的乘方可以通过快速幂的方法在 O(log⁡n)O(\log n) 的时间内获得。

# 代码

#include <iostream>
#include <vector>
using namespace std;
long long fibonacci(unsigned int n) {
    vector<int> result = {0, 1};
    if (n < 2) {
        return result[n];
    }
    long long first_term = 0;
    long long second_term = 1;
    long long n_th_term = 0;
    for (unsigned int i = 2; i <= n; ++i) {
        n_th_term = first_term + second_term;
        first_term = second_term;
        second_term = n_th_term;
    }
    return n_th_term;
}
# 题目二：青蛙跳台阶


一只青蛙一次可以跳上 11 级台阶，也可以跳上 22 级台阶。求该青蛙跳上一个 nn 级的台阶总共有多少种跳法。


# 思路


我们把 nn 级台阶时的跳法看成 nn 的函数，记为 f(n)f(n)。当 n>2n>2 时，第一次跳的时候就有两种不同的选择：一是第一次只跳 11 级，此时跳法数目等于后面剩下的 n−1n-1 级台阶的跳法数目，即为 f(n−1)f(n-1)；二是第一次跳 22 级，此时跳法数目等于后面剩下的 n−2n-2 级台阶的跳法数目，即为 f(n−2)f(n-2)。因此，nn 级台阶的不同跳法的总数 f(n)=f(n−1)+f(n−2)f(n)=f(n-1)+f(n-2)，不难看出这实际上就是斐波那契数列。


# 代码


略


# 面试题 11：旋转数组的最小数字


# 题目


把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 {3,4,5,1,2}\{3,4,5,1,2\} 为 {1,2,3,4,5}\{1,2,3,4,5\} 的一个旋转，该数组的最小值为 11。


# 思路


原来的数组是有序的，旋转之后的数组可以划分为两个有序的子数组，且第一个有序子数组的数字均大于第二个有序子数组。最小元素即这两个有序子数组的分界线。


用两个指针  left  和  right  分别指向数组的第一个元素和最后一个元素。按照题目中旋转的规则，第一个元素应该是大于或者等于最后一个元素。


接着可以找到数组中间的元素  mid 。如果  mid  位于前面的递增子数组，那么应当有  mid  ≥\ge  left 。此时数组中最小的元素应该位于  mid  的后面。可以把  left  指向  mid  指向的元素，这样可以缩小寻找的范围。移动之后的  left  指针仍然位于前面的递增子数组。


同样，如果  mid  位于后面的递增子数组，那么应当有  mid  ≤\le  right 。此时该数组中最小的元素应该位于  mid  的前面。我们可以把  right  指向  mid  指向的元素，这样也可以缩小寻找的范围。移动之后的  right  指针仍然位于后面的递增子数组。


按照上述思路， left  指针总是指向前面递增数组的元素，而  right  指针总是指向后面递增数组的元素。最终  left  指针将指向前面子数组的最后一个元素，而  right  指针会指向后面子数组的第一个元素。它们最终会指向两个相邻的元素，而第二个指针指向的刚好是最小的元素。这就是循环结束的条件。


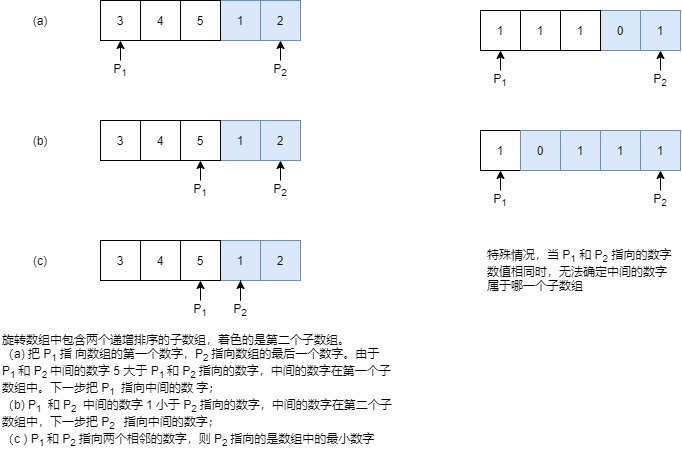
rotation_array


对于  left  指针和  right  指针指向的数字相同的情况，无法判断中间的数字属于哪一个子数组。此时必须采用顺序查找的办法，移动  left  或者  right  指针，直到两个指针指向的数字不相同。


# 代码


#include <iostream>
#include <vector>
using namespace std;
int find_min_inorder(vector<int> &numbers, int left_ptr, int right_ptr) {
    int ans = numbers[left_ptr];
    for (int i = left_ptr; i <= right_ptr; ++i) {
        if (ans > numbers[i]) {
            ans = numbers[i];
        }
    }
    return ans;
}
int find_min(vector<int> &numbers) {
    if (numbers.empty()) {
        throw "Invalid parameters";
    }
    int left_ptr = 0;
    int right_ptr = numbers.size() - 1;
    int mid_ptr = left_ptr;
    while (numbers[left_ptr] >= numbers[right_ptr]) {
        if (right_ptr - left_ptr == 1) {
            mid_ptr = right_ptr;
            break;
        }
        mid_ptr = left_ptr + (right_ptr - left_ptr) / 2;
        // 如果 left_ptr，right_ptr，mid_ptr 指向的三个数字相等，需要顺序查找
        if (numbers[left_ptr] == numbers[right_ptr] &&
            numbers[mid_ptr] == numbers[left_ptr]) {
            return find_min_inorder(numbers, left_ptr, right_ptr);
        }
        if (numbers[mid_ptr] >= numbers[left_ptr]) {
            left_ptr = mid_ptr;
        } else if (numbers[mid_ptr] <= numbers[right_ptr]) {
            right_ptr = mid_ptr;
        }
    }
    return numbers[mid_ptr];
}
# 面试题 12：矩阵中的路径


# 题目


请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。


# 思路


回溯法典型例题。在矩阵中任选一个点作为起点，进行深度优先遍历。第 ii 个各自对应于字符串的第 ii 个字符，如果两个字符不相同，那么该路径必然不是所求的目标路径。如果相同，那么以该位置作为起点，继续进行搜索。重复上述过程直到找到目标路径或者发现无目标路径。


由于路径不能重复经过某一个位置，因此还需要一个矩阵记录每个位置是否被访问过。


# 代码


#include <iostream>
#include <vector>
#include <string>
using namespace std;
bool has_path_core(const vector<vector<char>> &matrix, int i, int j, const string &str,
                   int &path_len, vector<vector<bool>> &visited) {
    if (str.size() == path_len) {
        return true;
    }
    int row = matrix.size();
    int col = matrix[0].size();
    bool is_has_path = false;
    if (i >= 0 && i < row && j >= 0 && j < col &&
        matrix[i][j] == str[path_len] &&
        visited[i][j] == false) {
        ++path_len;
        visited[i][j] = true;
        is_has_path = has_path_core(matrix, i, j - 1, str, path_len, visited) ||
                      has_path_core(matrix, i - 1, j, str, path_len, visited) ||
                      has_path_core(matrix, i, j + 1, str, path_len, visited) ||
                      has_path_core(matrix, i + 1, j, str, path_len, visited);
        if (is_has_path == false) {
            --path_len;
            visited[i][j] = false;
        }
    }
    return is_has_path;
}
bool has_path(vector<vector<char>> &matrix, const string &str) {
    if (matrix.empty() || matrix[0].size() == 0 || str.size() == 0) {
        return false;
    }
    int row = matrix.size();
    int col = matrix[0].size();
    vector<vector<bool>> visited(row, vector<bool>(col, false));
    int path_len = 0;
    for (int i = 0; i < row; ++i) {
        for (int j = 0; j < col; ++j) {
            if (has_path_core(matrix, i, j, str, path_len, visited)) {
                return true;
            }
        }
    }
    return false;
}
# 面试题 13：机器人的运动范围


# 题目


地上有一个 mm 行 nn 列的方格。一个机器人从坐标 (0,0)(0,0) 的格子开始移动，它每次可以向左、右、上、下移动一格，但不能进入行坐标和列坐标的数位之和大于 kk 的格子。例如，当 AA 为 1818 时，机器人能够进入方格 (35,37)(35,37)，因为 3+5+3+7=183+5+3+7=18。但它不能进入方格 (35，38)(35，38)，因为 3+5+3+8=193+5+3+8=19。请问该机器人能够到达多少个格子？


# 思路


机器人从坐标 (0,0)(0,0) 开始移动。当它准备进入坐标为 (i,j)(i,j) 的格子时，通过检査坐标的数位和来判断机器人是否能够进入。如果机器人能够进入坐标为 (i,j)(i, j) 的格子，则再判断它能否进入 44 个相邻的格子 (i,j−1)(i,j-1)、i−1,j)i-1,j)、(i,j+1)(i, j+1) 和 (i+1,j)(i+1,j)。


# 代码


#include <iostream>
#include <vector>
using namespace std;
int get_digit_sum(int number) {
    int sum = 0;
    while (number > 0) {
        sum += number % 10;
        number /= 10;
    }
    return sum;
}
bool check(int threshold, int rows, int cols, int i, int j, vector<vector<bool>> &visited) {
    if (i >= 0 && i < rows && j >= 0 && j < cols &&
            get_digit_sum(i) + get_digit_sum(j) <= threshold &&
            visited[i][j] == false) {
        return true;
    }
    return false;
}
int moving_count_core(int threshold, int rows, int cols, int i, int j, vector<vector<bool>> &visited) {
    int count = 0;
    if (check(threshold, rows, cols, i, j, visited)) {
        visited[i][j] = true;
        count = 1 + moving_count_core(threshold, rows, cols, i - 1, j, visited) +
                    moving_count_core(threshold, rows, cols, i, j - 1, visited) +
                    moving_count_core(threshold, rows, cols, i + 1, j, visited) +
                    moving_count_core(threshold, rows, cols, i, j + 1, visited);
    }
    return count;
}
int moving_count(int threshold, int rows, int cols) {
    if (threshold < 0 || rows <= 0 || cols <= 0) {
        return 0;
    }
    vector<vector<bool>> visited(rows, vector<bool>(cols, false));
    int count = moving_count_core(threshold, rows, cols, 0, 0, visited);
    return count;
}
# 面试题 14：剪绳子


# 题目


给定一根长度为 nn 的绳子，把绳子剪成 mm 段 （mm、nn 都是整数 n>1n>1 并且 m>1m>1），每段绳子的长度记为 k[0],k[1],⋯ ,k[m]k[0],k[1],\cdots,k[m]。请问 k[0]×k[1]×⋯×k[m]k[0]\times k[1] \times \cdots \times k[m] 可能的最大乘积是多少？例如，当绳子的长度是 8 时，我们把它剪成长度分别为 22、33、33 的三段，此时得到的最大乘积是 1818。


# 思路


# 动态规划


定义函数 f(n)f(n) 为把长度为 nn 的绳子剪成若干段后各段长度乘积的最大值。在剪第一刀的时候，有 n−1n-1 种可能的选择，因此 f(n)=arg max⁡if(i)×f(n−1),0<i<nf(n)=\argmax\limits_{i}{f(i)\times f(n-1)}, \quad 0<i<n。


这个公式如果直接计算，会有很多重复的子问题，造成大量不必要的计算。更好的方法是按照自底向上的顺序计算。


当绳子长度为 22 时，只可能将其剪成长度为 11 的两端，故 f(2)=1f(2)=1。当绳子长度为 33 时，有 1,2{1,2} 和 1,1,1{1,1,1} 两种方式，由于 1×2>1×1×11\times 2 > 1\times 1 \times 1，故 f(3)=2f(3) = 2。


# 贪心算法


一个满足题目所求的贪心方法是：当 n≥5n\ge5 时，尽可能多地将绳子剪长度为 33 的绳子；当剩余的绳子长度为 44 时，把绳子剪成长度为 22 的绳子。


原书上的证明过于简单，可以参考  LeetCode  上的链接。


# 代码


# 动态规划


#include <iostream>
using namespace std;
int cut_rope_dp(int length) {
    if (length < 2) {
        return 0;
    }
    if (length == 2) {
        return 1;
    }
    if (length == 3) {
        return 2;
    }
    vector<int> products(length + 1, 0);
    products[0] = 0;
    products[1] = 1;
    products[2] = 2;    // 这里为 2 是因为绳子长度大于 3，长度为 2 的绳子不剪时的乘积更大
    products[3] = 3;    // 理由同上
    int max_product = 0;
    for (int i = 4; i <= length; ++i) {
        max_product = 0;
        for (int j = 1; j <= i/2; ++j) {
            int product = products[i] * products[i - j];
            max_product = max(product, max_product);
            products[i] = max_product;
        }
    }
    max_product = products[length];
    return max_product;
}
# 贪心算法


int cut_rope_greedy(int length) {
    if (length < 2) {
        return 0;
    }
    if (length == 2) {
        return 1;
    }
    if (length == 3) {
        return 2;
    }
    // 尽可能多地剪去长度为 3 的绳子段
    int num_of_three = length / 3;
    // 当绳子最后的长度为 4 的时候，不能再剪去长度为 3 的绳子段
    // 因为剪成两端长度为 2 的绳子的乘积更大
    if (length - num_of_three * 3 == 1) {
        num_of_three -= 1;
    }
    int num_of_two = (length - num_of_three * 3) / 2;
    return static_cast<int>(pow(3, num_of_three)) * static_cast<int>(pow(2, num_of_two));
}
# 面试题 15：二进制中 11 的个数


# 题目


请实现一个函数，输入一个整数，输出该数二进制表示中 11 的个数。例如，把 99 表示成二进制是  1001 ， 有 22 位是 11。因此，如果输入 99，则该函数输出 22。


# 思路


常规思路是每次判断最低为是否为 11，判断之后进行右移运算。对于 3232 位的整数需要 3232 次循环。


除了这种方法之外，可以通过  n & (n-1)  快速计算。分析如下：


    

  • 如果一个整数不等于 00，那么该整数的二进制表示中至少有一位是 11。
    • 

  • 如果这个数的最右边一位是 11，那么减去 11 时，最后一位变成 00 而其他所有位都保持不变。也就是最后一位相当于做了取反操作，由 11 变成了 00。
    • 

  • 最后一位不是 11 而是 00 的情况。如果该整数的二进制表示中最右边的 11 位于第 mm 位，那么减去 11 时，第 mm 位由 11 变成 00，而第 mm 位之后的所有 00 都变成 11, 整数中第 mm 位之前的所有位都保持不变。举个例子：一个二进制数  1100 ，它的第二位是从最右边数起的一个 11。减去 11 后，第二位变成 00，它后面的两位 00 变成 11，而前面的 11 保持不变，因此得到的结果是  1011 。
    • 

  • 把一个整数减去 11，再和原整数做与运算，会把该整数最右边的 11 变成 00。
    • 



# 代码


#include <iostream>
using namespace std;
int number_of_one(int n) {
    int count = 0;
    while (n) {
        ++count;
        n = (n - 1) & n;
    }
    return count;
}